题目内容
集合M={a,b,c},N={-1,0,1},映射f:M→N满足f(a)+f(b)+f(c)=0,那么映射f:M→N的个数是多少?
解:∵f(a)∈N,f(b)∈N,f(c)∈N,
且f(a)+f(b)+f(c)=0,
∴有0+0+0=0+1+(-1)=0.
当f(a)=f(b)=f(c)=0时,只有一个映射;
当f(a)、f(b)、f(c)中恰有一个为0,而另两个分别为1,-1时,有C13·A22=6个映射.因此所求的映射的个数为1+6=7.
讲评:本题考查了映射的概念和分类讨论的思想,注意分类要全面,标准要统一.

练习册系列答案
相关题目
 {—6,—5,—4,—2, 1,3,4}.若关于x 的不等式
{—6,—5,—4,—2, 1,3,4}.若关于x 的不等式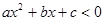 恒有实数解,则满足条件的集合M 的个数是
恒有实数解,则满足条件的集合M 的个数是