题目内容
5.任意四边形ABCD中,E,F分别是AD,BC的中点,若$\overrightarrow{EF}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{DC}$,则λ+μ=1.分析 可画出图形,取AB中点G,并连接EG,FG,从而EG,FG为两条中位线,从而可得到$\overrightarrow{EF}=\overrightarrow{GF}-\overrightarrow{GE}$,根据中位线的性质及向量加法的几何意义即可得出$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{DC}$,从而根据平面向量基本定理即可得出λ+μ=1.
解答 解:如图,取AB边中点G,连接EG,FG,则: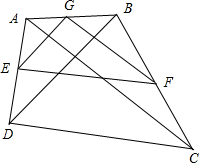
∵E,F分别是AD,BC的中点;
∴$\overrightarrow{EF}=\overrightarrow{GF}-\overrightarrow{GE}$=$\frac{1}{2}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{BD}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{DC})$$-\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{AD})=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{DC}$;
又$\overrightarrow{EF}=λ\overrightarrow{AB}+μ\overrightarrow{DC}$;
∴$λ=\frac{1}{2},μ=\frac{1}{2}$;
∴λ+μ=1.
故答案为:1.
点评 考查向量减法、加法和数乘的几何意义及其运算,三角形中位线的性质,以及平面向量基本定理.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
15.设a>0且a≠1,b∈R,则“a>1,0<b<1”是“函数y=loga(x+b),(x>-b)的图象同时经过第一、三、四象限”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.已知函数f(x)=2cosx-$\frac{1}{x}$,若$\frac{π}{3}$<a<b<$\frac{5π}{6}$,则( )
| A. | f(a)>f(b) | B. | f(a)<f(b) | C. | f(a)=f(b) | D. | f(a)f(b)>0 |