题目内容
中心在原点,焦点在x轴上的椭圆,短半轴长为1,当两准线间距离最小时,椭圆的方程为分析:先根据题意设出椭圆的标准方程,进而可用a表示出两准线间距离,进而根据函数的单调性,判断a2=2时,两准线距离最小,进而可得椭圆的方程.
解答:解:设椭圆的方程为
+y2=1
则两准线间距离d=2
=
=
∴当a2=2时,两准线的距离最小,
此时椭圆方程为
+y2=1
故答案为
+y2=1
| x2 |
| a 2 |
则两准线间距离d=2
| a2 |
| c |
| 2a2 | ||
|
|
∴当a2=2时,两准线的距离最小,
此时椭圆方程为
| x2 |
| 2 |
故答案为
| x2 |
| 2 |
点评:本题主要考查了椭圆的标准方程.解题的关键是通过设出椭圆的方程,利用a表示出两准线的距离,进而根据关于a的一元二次方程求得两准线距离的最小值.

练习册系列答案
相关题目
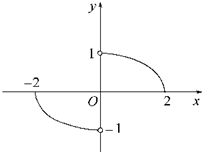 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|
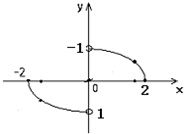 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
 .
.