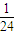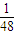题目内容
已知区域M:{(x,y)||x|+|y|≤2},N:{(x,y)|
},某人向区域M随机投掷一点P,则点P正好落在区域N的概率为( )
|
分析:区域M为正方形ABCD,区域N为两个弓形OE与OF的并集,以面积为测度,计算相应的面积,可求概率.
解答: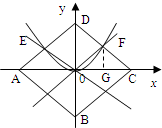 解:如图,∵区域M:{(x,y)||x|+|y|≤2},N:{(x,y)|
解:如图,∵区域M:{(x,y)||x|+|y|≤2},N:{(x,y)|
},
∴区域M为正方形ABCD,区域N为两个弓形OE与OF的并集.
SM=8,SN=2(S△OGF-
x2dx)=2(
-
)=
∴P=
=
故选A.
 解:如图,∵区域M:{(x,y)||x|+|y|≤2},N:{(x,y)|
解:如图,∵区域M:{(x,y)||x|+|y|≤2},N:{(x,y)|
|
∴区域M为正方形ABCD,区域N为两个弓形OE与OF的并集.
SM=8,SN=2(S△OGF-
| ∫ | 1 0 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
∴P=
| ||
| 8 |
| 1 |
| 24 |
故选A.
点评:本题主要考查了线性规划中的不等式表示的平面区域定积分求面积,以及几何概型,同时也考查了点集的交与并运算.

练习册系列答案
相关题目
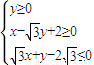 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率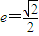 .
.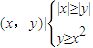 },某人向区域M随机投掷一点P,则点P正好落在区域N的概率为( )
},某人向区域M随机投掷一点P,则点P正好落在区域N的概率为( )