题目内容
在平面直角坐标系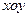 中,设二次函数
中,设二次函数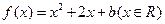 的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为
的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为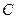 .
.
(I)求实数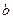 的取值范围;
的取值范围;
(II)求圆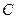 的一般方程;
的一般方程;
(III)圆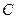 是否经过某个定点(其坐标与
是否经过某个定点(其坐标与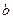 无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
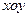 中,设二次函数
中,设二次函数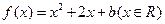 的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为
的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为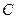 .
.(I)求实数
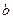 的取值范围;
的取值范围;(II)求圆
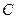 的一般方程;
的一般方程;(III)圆
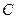 是否经过某个定点(其坐标与
是否经过某个定点(其坐标与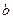 无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
无关)?若存在,请求出点点的坐标;若不存在,请说明理由.解:(I)令 得抛物线与
得抛物线与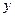 轴交点是
轴交点是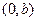 ;令
;令 ,由题意
,由题意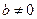 ,
,
且 ,解得
,解得 ,且
,且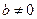 .
.
(II)设所求圆的一般方程为 ,
,
令 得,
得,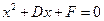 ,这与
,这与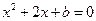 是同一个方程,故
是同一个方程,故 ,
,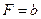 .
.
令 得,
得, ,此方程有一个根为
,此方程有一个根为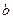 ,代入得出
,代入得出 ,
,
所以圆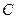 的一般方程为
的一般方程为 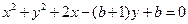 .
.
(III)圆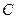 过定点
过定点 和
和 .
.
证明如下:
法1,直接将点的坐标代入验证;
法2,圆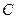 的方程改写为
的方程改写为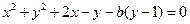 ,于是有
,于是有
 ,解得
,解得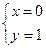 或
或 ,故过定点
,故过定点 和
和 .
.
 得抛物线与
得抛物线与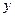 轴交点是
轴交点是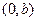 ;令
;令 ,由题意
,由题意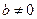 ,
,且
 ,解得
,解得 ,且
,且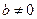 .
.(II)设所求圆的一般方程为
 ,
,令
 得,
得,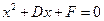 ,这与
,这与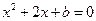 是同一个方程,故
是同一个方程,故 ,
,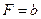 .
.令
 得,
得, ,此方程有一个根为
,此方程有一个根为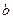 ,代入得出
,代入得出 ,
,所以圆
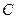 的一般方程为
的一般方程为 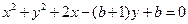 .
.(III)圆
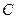 过定点
过定点 和
和 .
.证明如下:
法1,直接将点的坐标代入验证;
法2,圆
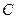 的方程改写为
的方程改写为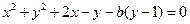 ,于是有
,于是有 ,解得
,解得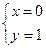 或
或 ,故过定点
,故过定点 和
和 .
.略

练习册系列答案
相关题目
 的定义域为( )
的定义域为( ) B.
B. C.
C. D.
D.
 且
且 。
。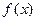 的解析式及定义域。(Ⅱ)求
的解析式及定义域。(Ⅱ)求 的定义域为R,则m的取值范围是
的定义域为R,则m的取值范围是  =
= ,其中
,其中 表示不超过x的最大整数,
表示不超过x的最大整数,  =1,
=1, =-2.当x∈
=-2.当x∈ ,
, (n∈
(n∈ )时,设函数
)时,设函数 ,则式子
,则式子 的最小值为 .
的最小值为 . 的定义域为( )
的定义域为( )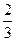 }
}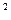 +bx+3a+b为偶函数,其定义域为 [ a—1, 2a ],则函数的值域为 。
+bx+3a+b为偶函数,其定义域为 [ a—1, 2a ],则函数的值域为 。