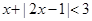题目内容
已知函数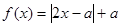 .
.
(1)若不等式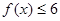 的解集为
的解集为 ,求实数
,求实数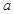 的值;
的值;
(2)在(Ⅰ)的条件下,若存在实数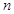 使
使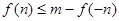 成立,求实数
成立,求实数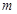 的取值范围.
的取值范围.
(1)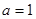 ;(2)
;(2)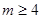
解析试题分析:(1)由|2x a|+a≤6得|2x a|≤6 a,再利用绝对值不等式的解法去掉绝对值,结合条件得出a值;(2)由(1)知f(x)="|2x" 1|+1,令φ(n)=f(n)+f( n),化简φ(n)的解析式,若存在实数n使f(n)≤m f( n)成立,只须m大于等于φ(n)的最小值即可,从而求出实数m的取值范围.
试题解析:(1)由 解得
解得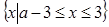
则 所以
所以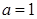 5分
5分
(2)由(1)知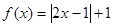
则原不等式为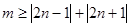 +2
+2
所以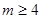 10分
10分
考点:绝对值不等式的解法

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
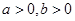 ,且
,且 ,若
,若 恒成立.
恒成立.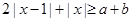 对任意的
对任意的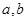 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围. x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围. 的不等式
的不等式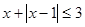 ;
;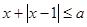 有解,求实数
有解,求实数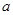 的取值范围.
的取值范围.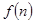 表示,且
表示,且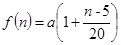 (其中
(其中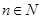 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元. +
+ +
+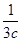 =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9.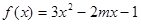 ,
,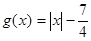 .
.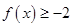 ;
;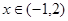 ,
,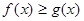 ,求
,求 的取值范围.
的取值范围.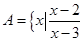 <
<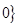 ,
,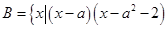 <
< 时,求
时,求 ;
;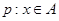 ,命题
,命题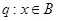 ,若q是p的必要条件,求实数
,若q是p的必要条件,求实数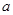 的取值范围.
的取值范围.