题目内容
.(本小题满分12分)
已知正项数列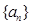 满足:
满足:
(1)求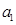 的范围,使得
的范围,使得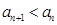 恒成立;
恒成立;
(2)若 ,证明
,证明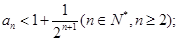
(3)若 ,证明:
,证明: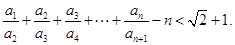
【答案】
解:(Ⅰ)由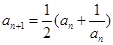 ,得
,得 由
由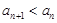 ,即
,即
所以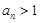 或
或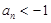 (舍)
(舍)
所以 时,
时,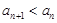 ……………3分
……………3分
(Ⅱ)证:若 ,得
,得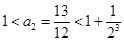 现假设
现假设 (
(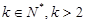 )
)
构造函数 ,易知
,易知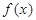 在
在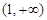 上单调增
上单调增
所以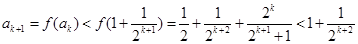
即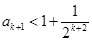
由以上归纳可知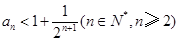 ……………6分
……………6分
(Ⅲ)由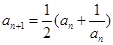 得
得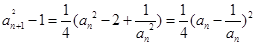
所以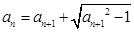
 ……………8分
……………8分
构造函数 ,
, 在
在 上单调递增
上单调递增
 所以
所以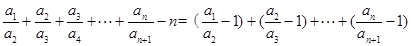
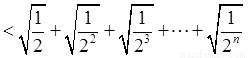
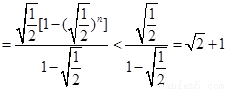 ……………12分
……………12分
【解析】略

练习册系列答案
相关题目