题目内容
空间直角坐标系中,棱长为6的正四面体ABCD的顶点A(0,0,0),B(0,6,0),C(3
,3,0),则正四面体的外接球球心O的坐标可以是( )
| 3 |
分析:如图所示,建立空间直角坐标系.设点G是底面正△ABC的中心,利用正三角形的性质可得G(
,3,0).取BC的中点E,连接AE、DE、DG,可得DG⊥平面ABC.可求出DE=3
,EG=
.在Rt△DEG中,DG,再利用OG2+GA2=DO2,即可得出.
| 3 |
| 3 |
| 3 |
解答:解:如图所示,建立空间直角坐标系.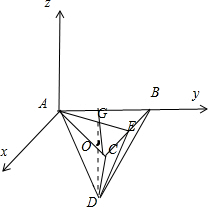
设点G是底面△ABC的中心,则G(
,3,0).
取BC的中点E,连接AE、DE、DG,则DG⊥平面ABC.
则DE=3
,EG=
,.
在Rt△DEG中,DG=
=2
.
∴OG2+GA2=DO2,即OG2+(2
)2=(2
-OG)2,
解得OG=
.
∴O(
,3,-
),
∴正四面体的外接球球心O的坐标可以是O(
,3,-
),
故选B.

设点G是底面△ABC的中心,则G(
| 3 |
取BC的中点E,连接AE、DE、DG,则DG⊥平面ABC.
则DE=3
| 3 |
| 3 |
在Rt△DEG中,DG=
| DE2-EG2 |
| 6 |
∴OG2+GA2=DO2,即OG2+(2
| 3 |
| 6 |
解得OG=
| ||
| 2 |
∴O(
| 3 |
| ||
| 2 |
∴正四面体的外接球球心O的坐标可以是O(
| 3 |
| ||
| 2 |
故选B.
点评:本题考查了正四面体的性质、正三角形的性质、勾股定理等基础知识与基本方法,属于难题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
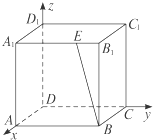
 如图,在空间直角坐标系中,正方体棱长为2,点E是棱AB的中点,点F(0,y,z)是正方体的面AA1D1D上点,且CF⊥B1E,则点F(0,y,z)满足方程( )
如图,在空间直角坐标系中,正方体棱长为2,点E是棱AB的中点,点F(0,y,z)是正方体的面AA1D1D上点,且CF⊥B1E,则点F(0,y,z)满足方程( )| A、y-z=0 | B、2y-z-1=0 | C、2y-z-2=0 | D、z-1=0 |
如图,在空间直角坐标系中,正方体ABCDA1B1C1D1的棱长为1,B1E=
A1B1,则
等于( )
| 1 |
| 4 |
| BE |

A、(0,
| ||
B、(-
| ||
C、(0,-
| ||
D、(
|