Question

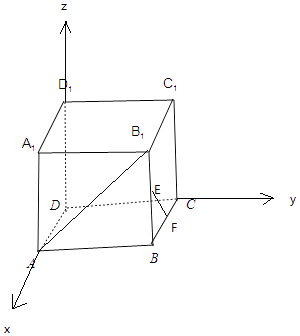
【题目】在正方体ABCD﹣A1B1C1D1中，E、F分别为棱BB1、BC的中点，则异面直线AB1与EF所成角的大小为（ ）
A.30°
B.45°
C.60°
D.90°

Answer 1

【答案】C
【解析】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，

设正方体ABCD﹣A1B1C1D1中棱长为2，

则A（2，0，0），B1（2，2，2），E（2，2，1），F（1，2，0），

=（0，2，2）， =（﹣1，0，﹣1），

设异面直线AB1与EF所成角的大小为θ，

则cosθ=|cos＜ ＞|= = = ，

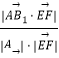∴θ=60°，

∴异面直线AB1与EF所成角的大小为60°．

故选：C．

【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．