题目内容
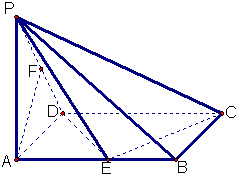
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点.(1)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(2)若点E为PC的中点,求证PA∥平面BDE;
(3)求由点A绕四棱锥P-ABCD的侧面一周回到点A的最短距离.
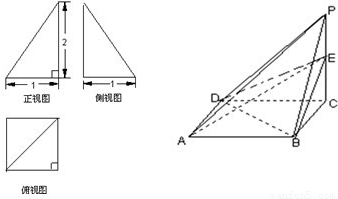
【答案】分析:(1)由ABCD是正方形可得BD⊥AC,由PC⊥底面ABCD可得BD⊥PC,由线面垂直的判定定理得BD⊥平面PAC,进而由线面垂直的性质得到不论点E在何位置,都有BD⊥AE
(2)连接AC交BD于F,连接EF,由中位线定理及线面平行的判定定理可证得PA∥平面BDE;
(3)(3)将四棱锥的侧面沿PA展开,将空间问题转化为平面上两点之间线段最短,解△PAA′可得答案.
解答: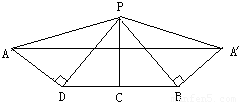 解:(1)不论点E在何位置,都有BD⊥AE
解:(1)不论点E在何位置,都有BD⊥AE
证明如下:连接AC,
∵ABCD是正方形
∴BD⊥AC
∵PC⊥底面ABCD 且BD?平面ABCD
∴BD⊥PC …(2分)
又∵AC∩PC=C
∴BD⊥平面PAC …(3分)
∵不论点E在何位置,都有AE?平面PAC
∴不论点E在何位置,都有BD⊥AE …(4分)
证明:(2)连接AC交BD于F,连接EF,则点F为BD的中点,
又点E为PC的中点,
∴EF∥PA,
又EF?平面BDE,
∴PA∥平面BDE…(9分)
(3)将四棱锥的侧面沿PA展开,如图示,则AA′即为所求.
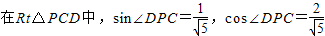 ;
;
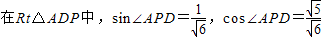 ;
;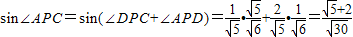 ;…(12分)
;…(12分)
∴ ;…(14分)
;…(14分)
点评:本题考查的知识点是直线与平面垂直的性质及判定定理,直线与平面平行的判定定理,多面体表面上的最短距离问题,是立体几何线面关系及转化思想的综合应用,难度中档.
(2)连接AC交BD于F,连接EF,由中位线定理及线面平行的判定定理可证得PA∥平面BDE;
(3)(3)将四棱锥的侧面沿PA展开,将空间问题转化为平面上两点之间线段最短,解△PAA′可得答案.
解答:
 解:(1)不论点E在何位置,都有BD⊥AE
解:(1)不论点E在何位置,都有BD⊥AE证明如下:连接AC,
∵ABCD是正方形
∴BD⊥AC
∵PC⊥底面ABCD 且BD?平面ABCD
∴BD⊥PC …(2分)
又∵AC∩PC=C
∴BD⊥平面PAC …(3分)
∵不论点E在何位置,都有AE?平面PAC
∴不论点E在何位置,都有BD⊥AE …(4分)
证明:(2)连接AC交BD于F,连接EF,则点F为BD的中点,
又点E为PC的中点,
∴EF∥PA,
又EF?平面BDE,
∴PA∥平面BDE…(9分)
(3)将四棱锥的侧面沿PA展开,如图示,则AA′即为所求.
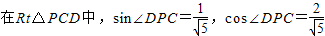 ;
;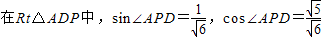 ;
;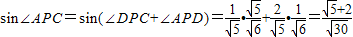 ;…(12分)
;…(12分)∴
 ;…(14分)
;…(14分)点评:本题考查的知识点是直线与平面垂直的性质及判定定理,直线与平面平行的判定定理,多面体表面上的最短距离问题,是立体几何线面关系及转化思想的综合应用,难度中档.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD, 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点. (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点. (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点.