题目内容
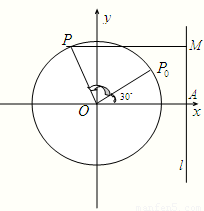
如图,圆O的半径为2,P是圆上的动点,Q(6,0)是x轴上的定点,M是PQ的中点.当点P绕O作匀速圆周运动时,求点M的轨迹的参数方程.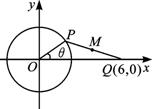
思路分析:取∠xOP=θ为参数,则圆O的参数方程是![]() (θ为参数),当θ变化时,动点P在定圆O上运动,线段PQ也随之变动,从而使点M运动. 所以,点M的运动可以看成是由角θ决定的.于是,选θ为参数是合适的.
(θ为参数),当θ变化时,动点P在定圆O上运动,线段PQ也随之变动,从而使点M运动. 所以,点M的运动可以看成是由角θ决定的.于是,选θ为参数是合适的.
解:设点M的坐标是(x,y),∠xOP=θ,则点P的坐标是(2 cosθ,2 sinθ).由中点坐标公式可得x=![]() =cosθ+3,y=
=cosθ+3,y=![]() =sinθ.
=sinθ.
所以,点M的轨迹的参数方程是
![]() (θ为参数).
(θ为参数).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
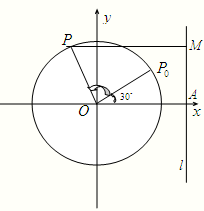 如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且
如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且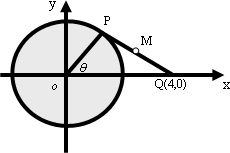
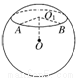
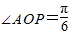 ,点P从P处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.
,点P从P处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.