题目内容
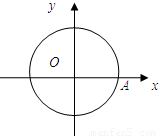
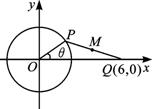
 如图,圆O的方程为x2+y2=4,(1)已知点A的坐标为(2,0),B为圆周上任意一点,求弧
如图,圆O的方程为x2+y2=4,(1)已知点A的坐标为(2,0),B为圆周上任意一点,求弧 长小于π的概率;(2)若P(x,y)为圆O内任意一点,求P到原点的距离大于1的概率.
长小于π的概率;(2)若P(x,y)为圆O内任意一点,求P到原点的距离大于1的概率.
解:(1)圆O的周长为4π,
∴弧 长小于π的概率
长小于π的概率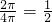 ,
,
(2)记事件A为P到原点的距离大于1,则Ω(A)={(x,y)|x2+y2>1},
Ω={(x,y)|x2+y2≤4},
∴P(A)=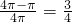
分析:(1)由已知中点A为周长等于3的圆周上的一个定点,我们求出劣弧AB长度小于1时,B点所在位置对应的弧长,然后代入几何概型公式,即可得到答案.
点评:本题考查的知识点是几何概型,其中计算出所有事件和满足条件的事件对应的几何量的值是解答此类问题的关键.属基础题.
∴弧
 长小于π的概率
长小于π的概率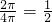 ,
,(2)记事件A为P到原点的距离大于1,则Ω(A)={(x,y)|x2+y2>1},
Ω={(x,y)|x2+y2≤4},
∴P(A)=
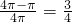
分析:(1)由已知中点A为周长等于3的圆周上的一个定点,我们求出劣弧AB长度小于1时,B点所在位置对应的弧长,然后代入几何概型公式,即可得到答案.
点评:本题考查的知识点是几何概型,其中计算出所有事件和满足条件的事件对应的几何量的值是解答此类问题的关键.属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
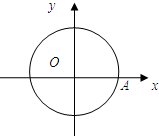 如图,圆O的方程为x2+y2=4,
如图,圆O的方程为x2+y2=4,
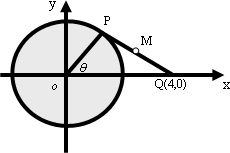
 长小于π的概率;
长小于π的概率;