题目内容
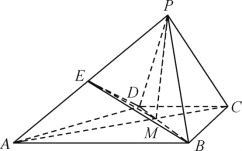
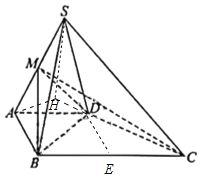
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,CD=SD,点M是SA的中点,AD//BC,∠ABC=90°,AB=AD![]() BC=a.
BC=a.
(1)求证:平面MBD⊥平面SCD;
(2)若∠SDC=120°,求三棱锥C﹣MBD的体积.
【答案】(1)证明见解析;(2)![]() a3.
a3.
【解析】
(1)取BC中点E,连接DE,则AB=AD=a,BC=2a.由题意可得:四边形ABED为正方形,可得BD2+CD2=BC2,于是BD⊥CD,根据面面垂直的性质定理可得:BD⊥平面SCD,进而得出平面MBD⊥平面SCD.
(2)过点S作SH⊥CD,交CD的延长线于点H,连接AH.∠SDH为SD与底面ABCD所成的角,即∠SDH=60°.点M到平面ABCD的距离d=SH.可得三棱锥C﹣MBD的体积V![]() BD×CD
BD×CD![]() d.
d.
(1)证明:取BC中点E,连接DE,则AB=AD=a,BC=2a.由题意可得:四边形ABED为正方形,且BE=DE=CE=a,BD=CD![]() a.
a.
∴BD2+CD2=BC2,则BD⊥CD,又平面SCD⊥平面ABCD,平面SCD∩平面ABCD=CD,
∴BD⊥平面SCD,BD平面MBD,∴平面MBD⊥平面SCD.
(2)解:过点S作SH⊥CD,交CD的延长线于点H,连接AH.
则∠SDH为SD与底面ABCD所成的角,即∠SDH=60°.
由(1)可得:SD=CD![]() a,∴在Rt△SHD中,SD
a,∴在Rt△SHD中,SD![]() a,HD
a,HD![]() a,SH
a,SH![]() a.
a.
∴点M到平面ABCD的距离d![]() a.
a.
∴三棱锥C﹣MBD的体积V![]() BD×CDd
BD×CDd![]() a3.
a3.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】随着城市化、工业化进程加速,汽车工业快速发展,国际原油供求矛盾逐步加深,全球气候变暖日益明显.在此背景下,以节能减排为重要目标的新能源汽车技术不断取得突破,并呈现快速突破、竞相发展的态势.在2015年10月份,国家发改委等部委在《电动汽车充电基础设施发展指南(2015-2020年)》中要求,新建住宅配建停车位应100%建设充电基础设施或预留建设安装条件,大型公共建筑物配建停车场、社会公共停车场建设充电基础设施或预留建设安装条件的车位比例不低于10%,每2000辆电动汽车应至少配套建设一座公共充电站.
为鼓励新能源汽车发展,国家和地方出台了相关补贴政策.
附表1:2018年某市新能源汽车补贴政策:
纯电续航里程( | 国家补贴(万元/辆) | 地方补贴(万元/辆) |
| 1.50 | 0.75 |
| 2.4 | 1.2 |
| 3.4 | 1.7 |
| 4.5 | 2.25 |
| 5 | 2.5 |
为了获得更大的市场分额,抢占未来新能源汽车销售先机.该市对2018年各类型新能源汽车销售占比情况进行了调查.
附表2:2018年该市各类型新能源汽车销售占比情况:
纯电续航里程 |
|
|
|
|
|
占比 | 5% | 20% | 35% | 25% | 15% |
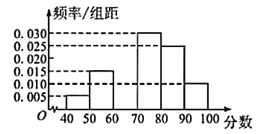
(1)用2018年新能源汽车销售占比来估计2019年的新能源汽车销售情况,求2019年每辆新能源汽车的平均补贴.若该市2019年想实现3000万元补贴,估计需要销售新能源汽车多少量.(补贴政策按每辆车补贴=国家补贴+地方补贴,结果四舍五入保留整数)
(2)该市新能源汽车促进办公宝为了调查新能源汽车补贴发放情况,希望从2018年销售的新能漂源汽车中抽取10辆车的信息进行回访核实.以各类型新能源汽车销售占比为概率.求抽到几辆续航里程小于![]() 新能源汽车的可能性最大.
新能源汽车的可能性最大.