题目内容
函数f(x)=ax3﹣6ax2+3bx+b,其图象在x=2处的切线方程为3x+y﹣11=0.
(1)求函数f(x)的解析式;
(2)若函数y=f(x)的图象与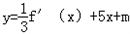 的图象有三个不同的交点,求实数m的取值范围.
的图象有三个不同的交点,求实数m的取值范围.
(1)求函数f(x)的解析式;
(2)若函数y=f(x)的图象与
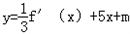 的图象有三个不同的交点,求实数m的取值范围.
的图象有三个不同的交点,求实数m的取值范围.解:(1)由题意得f'(x)=3ax2﹣12ax+3b,f'(2)=﹣3且f(2)=5,
∴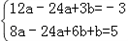 即
即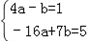 解得a=1,b=3,
解得a=1,b=3,
∴f(x)=x3﹣6x2+9x+3.
(2)由f(x)=x3﹣6x2+9x+3,
可得f'(x)=3x2﹣12x+9,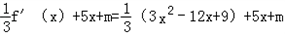 =x2+x+3+m,
=x2+x+3+m,
则由题意可得x3﹣6x2+9x+3=x2+x+3+m有三个不相等的实根,
即g(x)=x3﹣7x2+8x﹣m的图象与x轴有三个不同的交点,
g'(x)=3x2﹣14x+8=(3x﹣2)(x﹣4),
则g(x),g'(x)的变化情况如下表.

则函数f(x)的极大值为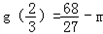 ,极小值为g(4)=﹣16﹣m.
,极小值为g(4)=﹣16﹣m.
y=f(x)的图象与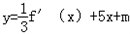 的图象有三个不同交点,
的图象有三个不同交点,
则有: 解得
解得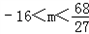 .
.
∴
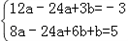 即
即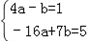 解得a=1,b=3,
解得a=1,b=3,∴f(x)=x3﹣6x2+9x+3.
(2)由f(x)=x3﹣6x2+9x+3,
可得f'(x)=3x2﹣12x+9,
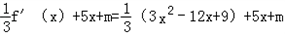 =x2+x+3+m,
=x2+x+3+m,则由题意可得x3﹣6x2+9x+3=x2+x+3+m有三个不相等的实根,
即g(x)=x3﹣7x2+8x﹣m的图象与x轴有三个不同的交点,
g'(x)=3x2﹣14x+8=(3x﹣2)(x﹣4),
则g(x),g'(x)的变化情况如下表.

则函数f(x)的极大值为
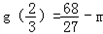 ,极小值为g(4)=﹣16﹣m.
,极小值为g(4)=﹣16﹣m.y=f(x)的图象与
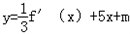 的图象有三个不同交点,
的图象有三个不同交点,则有:
 解得
解得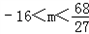 .
.
练习册系列答案
相关题目