题目内容
【题目】已知定义在![]() 上的数
上的数![]() 满足
满足![]() ,当
,当![]() 时
时![]() .若关于
.若关于![]() 的方程
的方程![]() 有三个不相等的实数根,则实数
有三个不相等的实数根,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
根据f(2﹣x)=f(2+x)可知函数f(x)关于x=2对称,利用当![]() 时
时![]() ,画出函数y=f(x)的大致图象.由题意转化为y=k(x﹣2)+e﹣1与f(x)有三个交点,直线恒过定点(2,e﹣1),再根据数形结合法可得k的取值范围.
,画出函数y=f(x)的大致图象.由题意转化为y=k(x﹣2)+e﹣1与f(x)有三个交点,直线恒过定点(2,e﹣1),再根据数形结合法可得k的取值范围.
由题意,当x≤2时,f(x)=(x﹣1)ex﹣1.f′(x)=xex.
①令f′(x)=0,解得x=0;②令f′(x)<0,解得x<0;③令f′(x)>0,解得0<x≤2.
∴f(x)在(﹣∞,0)上单调递减,在(0,2]上单调递增,
在x=0处取得极小值f(0)=﹣2.且f(1)=﹣1;x→﹣∞,f(x)→0.
又∵函数f(x)在R上满足f(2﹣x)=f(2+x),∴函数f(x)的图象关于x=2对称.
∴函数y=f(x)的大致图象如图所示:
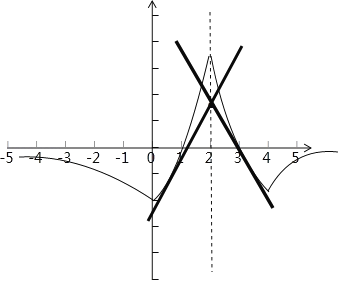
关于x的方程f(x)﹣kx+2k﹣e+1=0可转化为f(x)=k(x﹣2)+e﹣1.
而一次函数y=k(x﹣2)+e﹣1很明显是恒过定点(2,e﹣1).结合图象,当k=0时,有两个交点,不符合题意,
当k=e时,有两个交点,其中一个是(1,﹣1).此时y=f(x)与y=k(x﹣2)+e﹣1正好相切.
∴当0<k<e时,有三个交点.同理可得当﹣e<k<0时,也有三个交点.
实数k的取值范围为:(﹣e,0)∪(0,e).
故选:D.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目