题目内容
已知2x≤256且log2x≥| 1 |
| 2 |
| x |
| 2 |
| 2 |
| ||
| 2 |
分析:由2x≤256且log2x≥
,可解得
≤x≤8,即函数f(x)=log2
•log
的定义域为[
,8],对函数表达式进行化简、配方,而后判断求值.
| 1 |
| 2 |
| 2 |
| x |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
解答:解:由2x≤256且log2x≥
,可解得
≤x≤8,
则f(x)的定义域为[
,8],
f(x)=log2
•log
=(log2x-1)×(log2x-2)=(log2x-
) 2-
由f(x)的定义域为[
,8],即3≥log2x≥
故函数的最大值是f(8)=2
最小值是-
答:函数f(x)=log2
•log
的最大值和最小值分别为2与-
.
| 1 |
| 2 |
| 2 |
则f(x)的定义域为[
| 2 |
f(x)=log2
| x |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
由f(x)的定义域为[
| 2 |
| 1 |
| 2 |
故函数的最大值是f(8)=2
最小值是-
| 1 |
| 4 |
答:函数f(x)=log2
| x |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
点评:本题考查解指数不等式与对数不等式的解法,以及求对数函数的最值,主要训练根据运算性质灵活变形的能力.本题在求最值时用到了配方法,配方法是求最值的常用手段.

练习册系列答案
相关题目
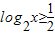 ,求函数
,求函数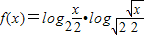 的最大值和最小值.
的最大值和最小值.