题目内容
9．
如图，四面体ABCD的各棱长均为a，E、F分别是AB、CD的中点．（1）证明：线段EF是异面直线AB与CD的公垂线段；
（2）求异面直线AB与CD的距离．
分析 （1）连结AF，BF，证明EF与AB，CD垂直且相交，即可得出结论；
（2）在Rt△AEF中，根据勾股定理可求出所求．
解答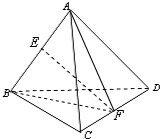 
（1）证明：连结AF，BF．
由△ACD，△BCD为等边三角形，F为CD的中点，
∴AF=BF．
又E为CD的中点，
∴EF⊥AB．
同理，EF⊥CD．
又EF与AB，CD都相交，故线段EF是异面直线AB与CD的公垂线段．
（2）在Rt△AEF中，AF=$\frac{\sqrt{3}}{2}$a，AE=$\frac{1}{2}$a，
∴EF=$\frac{\sqrt{2}}{2}$a
故异面直线AB与CD的距离为$\frac{\sqrt{2}}{2}$a．
点评 本题主要考查异面直线公垂线的证明、距离的计算，比较基础．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，侧棱PA⊥底面ABCD，AD∥BC，∠ABC=90°，PA=AB=BC=2，AD=1，M是棱PB中点．
如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的四个顶点所构成的菱形的边长是$\sqrt{5}$，面积是4，圆R：（x-4）2+y2=r2（6＞r＞2）与椭圆C交于点M与点N，连接RM并延长交椭圆于点P．
17．函数f（x）=x3+2ax2+x在（0，+∞）有两个极值点，则实数a的取值范围是（ ）
| A． | （0，+∞） | B． | （-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$） | C． | （-$∞，-\frac{\sqrt{3}}{2}$） | D． | （-∞，0） |
如图，在三棱锥P-ABC中，PA=1，PB=PC=BC=2，AB=AC=$\sqrt{3}$，