题目内容
已知空间四边形ABCD中,E、H分别是AB、AD的中点.
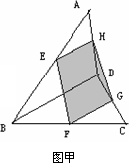
(1)如图(甲)中,F、G分别是BC、CD的中点,求证:四边形EFGH是平行四边形;
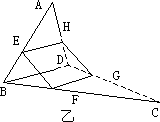
(2)如图(乙)中,若F是BC上的点,G是DC上的点,且![]() ,求证:四边形EFGH是梯形,并且直线EF、GH、AC共点.
,求证:四边形EFGH是梯形,并且直线EF、GH、AC共点.
答案:
解析:
解析:
|
证明:(1)如图(甲),连结BD. ∵EH是的△ABD中位线, ∴EH 根据公理4,EH ∴四边形EFGH是平行四边形. (2)如图(乙)由(1)知EH ∴FG∥BD,FG= 由公理4,∴EH∥FG,又FG>EH. ∴四边形EFGH是梯形. 则直线EF、GH相交,设EF∩GH=P 则P∈EF,又EF ∴P∈平面ABC,同理P∈平面ADC. 又平面ABC∩平面ADC=AC 由公理2,得P∈AC, 即EF、GH、AC三条直线共点. 点评:证明四边形是平行四边形或者梯形,首先必须证明它是平面图形,本题中的EH∥FG是关键 |

练习册系列答案
相关题目
 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证:
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证:
