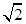题目内容
求满足下列条件的直线 方程(13分)
方程(13分)
(1)直线 过原点且与直线
过原点且与直线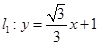 的夹角为
的夹角为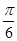 ;
;
(2)直线 过直线
过直线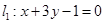 与
与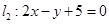 的交点,且点
的交点,且点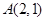 到
到 的距离为
的距离为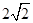 .
.
 方程(13分)
方程(13分)(1)直线
 过原点且与直线
过原点且与直线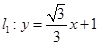 的夹角为
的夹角为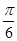 ;
;(2)直线
 过直线
过直线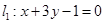 与
与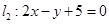 的交点,且点
的交点,且点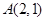 到
到 的距离为
的距离为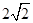 .
.(1)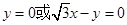 ;(2)
;(2)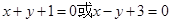 。
。
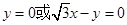 ;(2)
;(2)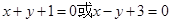 。
。本题考查直线方程的求法,是基础题.解题时要认真审题,注意直线与直线垂直、直线与直线平行、直线交点等知识点的合理运用.
(1)因为直线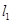 的倾斜角为
的倾斜角为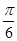 ,由条件,直线
,由条件,直线 的倾斜角应为
的倾斜角应为 或
或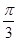 ,所以直线
,所以直线 的斜率
的斜率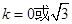 ,又直线
,又直线 过原点,所以直线
过原点,所以直线 的方程为:
的方程为:
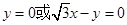
(2)由条件设直线 为
为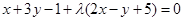 ,整理得
,整理得
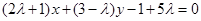 ,点
,点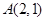 到
到 的距离为
的距离为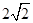
解:(1)直线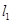 的倾斜角为
的倾斜角为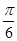 ,由条件,直线
,由条件,直线 的倾斜角应为
的倾斜角应为 或
或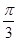 ,所以直线
,所以直线 的斜率
的斜率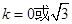 ,又直线
,又直线 过原点,所以直线
过原点,所以直线 的方程为:
的方程为:
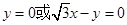
(2)由条件设直线 为
为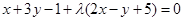 ,整理得
,整理得
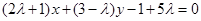 ,点
,点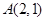 到
到 的距离为
的距离为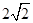 ,则
,则
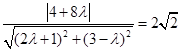 ,解得
,解得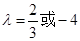 ,所以直线
,所以直线 为
为
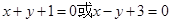
(1)因为直线
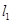 的倾斜角为
的倾斜角为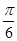 ,由条件,直线
,由条件,直线 的倾斜角应为
的倾斜角应为 或
或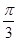 ,所以直线
,所以直线 的斜率
的斜率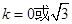 ,又直线
,又直线 过原点,所以直线
过原点,所以直线 的方程为:
的方程为: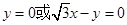
(2)由条件设直线
 为
为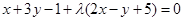 ,整理得
,整理得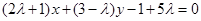 ,点
,点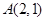 到
到 的距离为
的距离为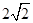
解:(1)直线
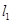 的倾斜角为
的倾斜角为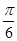 ,由条件,直线
,由条件,直线 的倾斜角应为
的倾斜角应为 或
或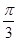 ,所以直线
,所以直线 的斜率
的斜率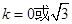 ,又直线
,又直线 过原点,所以直线
过原点,所以直线 的方程为:
的方程为: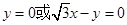
(2)由条件设直线
 为
为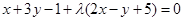 ,整理得
,整理得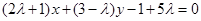 ,点
,点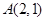 到
到 的距离为
的距离为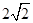 ,则
,则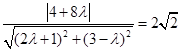 ,解得
,解得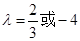 ,所以直线
,所以直线 为
为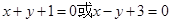

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
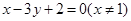
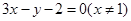
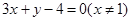
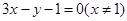
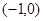 ,且与直线
,且与直线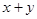 =0垂直的直线方程是
=0垂直的直线方程是  ,其倾斜角的大小是( )
,其倾斜角的大小是( ) :
: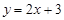 ,直线
,直线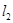 与
与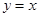 对称,直线
对称,直线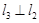 ,则
,则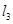 的斜率为( )
的斜率为( )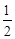
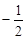
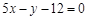 ,BC:
,BC: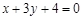
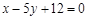 ,
,