题目内容
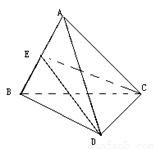
已知空间四边形ABCD中,AC,BD成60°角,且AC=4,BD=2| 3 |
分析:根据三角形的中位线定理知,∠EFG即为AC,BD成60°的角,且EF、EH的长为其第三边的一半,根据平行四边形的面积公式即得.
解答: 解:如图,在平行四边形EFGH中,EF=
解:如图,在平行四边形EFGH中,EF=
AC=2,EH=
BD=
,
∠EFG=60°,
∴四边形EFGH的面积为:
EF×EH×sin∠EFG=2×
×
=3.
故答案为:3.
 解:如图,在平行四边形EFGH中,EF=
解:如图,在平行四边形EFGH中,EF=| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∠EFG=60°,
∴四边形EFGH的面积为:
EF×EH×sin∠EFG=2×
| 3 |
| ||
| 2 |
故答案为:3.
点评:本题主要考查了棱锥的结构特征,以及异面直线及其所成的角,属于基础题.

练习册系列答案
相关题目
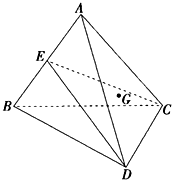
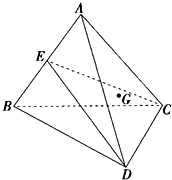 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证:
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证: