题目内容
已知函数f(x)=lnx-ax+1(x>0)
(1)若对任意的x∈[1,+∞),f(x)≤0恒成立,求实数a的最小值.
(2)若a=
且关于x的方程f(x)=-
x2+b在[1,4]上恰有两个不相等的实数根,求实数b的取值范围.
(1)若对任意的x∈[1,+∞),f(x)≤0恒成立,求实数a的最小值.
(2)若a=
| 5 |
| 2 |
| 1 |
| 2 |
分析:(1)利用参变量分离法将恒成立转化为求函数的最值问题,再利用导数求出最值,列出不等关系,即可求得a的取值范围,从而得到实数a的最小值;
(2)利用参变量分离法转化为b=
x2+lnx-
x+1,x∈[1,4]有两个不等的实根,令h(x)=b=
x2+lnx-
x+1,再将方程有两个不等的实数根转化为函数y=b与y=h(x)在[1,4]上有两个不同的交点,再结合图象即可求得实数b的取值范围.
(2)利用参变量分离法转化为b=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答:解:(1)∵对任意的x∈[1,+∞),f(x)=lnx-ax+1≤0恒成立,
∴a≥
在[1,+∞)上恒成立,
令g(x)=
,x∈[1,+∞),
则g′(x)=
=0,解得x=1,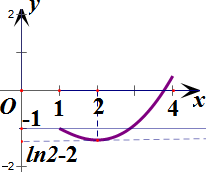
当x∈(1,+∞)时,g′(x)<0,即g(x)在(1,+∞)上单调递减,
∴g(x)在[1,+∞)上的最大值为g(1)=1,
∴a≥1,即实数a的最小值为1;
(2)∵a=
,f(x)=-
x2+b,
∴b=
x2+lnx-
x+1,x∈[1,4]有两个不等的实根,
令h(x)=
x2+lnx-
x+1,x∈[1,4],
∴h′(x)=x+
-
=
=
,
令h′(x)=0,则x=
(舍)或x=2,
∴h(x)在(1,2)上单调递减,在(2,4)上单调递增,
∴h(x)在x=2处取得极小值h(2)=ln2-2,又h(1)=-1,h(4)=ln4-1>-1=h(1),
要使b=
x2+lnx-
x+1,x∈[1,4]有两个不等的实根,
则y=b与y=h(x)的图象在x∈[1,4]有两个不同的交点,
结合图象可知,ln2-2<b≤-1,
故实数b的取值范围是ln2-2<b≤-1.
∴a≥
| lnx+1 |
| x |
令g(x)=
| lnx+1 |
| x |
则g′(x)=
| ||
| x2 |

当x∈(1,+∞)时,g′(x)<0,即g(x)在(1,+∞)上单调递减,
∴g(x)在[1,+∞)上的最大值为g(1)=1,
∴a≥1,即实数a的最小值为1;
(2)∵a=
| 5 |
| 2 |
| 1 |
| 2 |
∴b=
| 1 |
| 2 |
| 5 |
| 2 |
令h(x)=
| 1 |
| 2 |
| 5 |
| 2 |
∴h′(x)=x+
| 1 |
| x |
| 5 |
| 2 |
| 2x2-5x+2 |
| 2x |
| (x-2)(2x-1) |
| 2x |
令h′(x)=0,则x=
| 1 |
| 2 |
∴h(x)在(1,2)上单调递减,在(2,4)上单调递增,
∴h(x)在x=2处取得极小值h(2)=ln2-2,又h(1)=-1,h(4)=ln4-1>-1=h(1),
要使b=
| 1 |
| 2 |
| 5 |
| 2 |
则y=b与y=h(x)的图象在x∈[1,4]有两个不同的交点,
结合图象可知,ln2-2<b≤-1,
故实数b的取值范围是ln2-2<b≤-1.
点评:本题考查了利用导数研究函数的最值,利用导数研究函数的单调性与极值,从而得到函数的简图,同时考查了函数的零点与方程的根的关系,将方程有解问题转化为函数的图象有交点进行解决.属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目