题目内容
已知四点O(0,0),A(t,1),B(2,3),C(6,t),其中t∈R.若四边形OACB是平行四边形,且点P(x,y)在其内部及其边界上,则2y-x的最小值是 .
【答案】分析:根据向量相等的方法算出然后t=4,从而得到A、B、C各点的坐标,再作出平行四边形OACB如图,将目标函数z=2x-y对应的直线进行平移,可得当x=4,y=1时,z=2x-y取得最小值为-2.
解答:解:∵四边形OACB是平行四边形
∴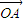 =
= ,可得(t,1)=(6-2,t-3),解之得t=4
,可得(t,1)=(6-2,t-3),解之得t=4
由此得到各点坐标:A(4,1),B(2,3),C(6,4)
作出平行四边形OACB如图,
设z=F(x,y)=2x-y,将直线l:z=2x-y进行平移,
当l经过点A时,目标函数z达到最大值
∴z最小值=F(4,1)=-2
故答案为:-2
点评:本题给出平行四边形及其内部作为可行域,求目标函数z=2x-y的最小值,着重考查了向量相等的坐标运算、二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.
解答:解:∵四边形OACB是平行四边形

∴
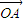 =
= ,可得(t,1)=(6-2,t-3),解之得t=4
,可得(t,1)=(6-2,t-3),解之得t=4由此得到各点坐标:A(4,1),B(2,3),C(6,4)
作出平行四边形OACB如图,
设z=F(x,y)=2x-y,将直线l:z=2x-y进行平移,
当l经过点A时,目标函数z达到最大值
∴z最小值=F(4,1)=-2
故答案为:-2
点评:本题给出平行四边形及其内部作为可行域,求目标函数z=2x-y的最小值,着重考查了向量相等的坐标运算、二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
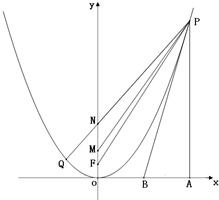 已知四点O(0,0),
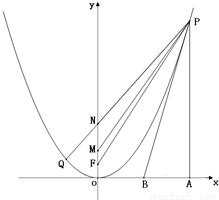
已知四点O(0,0),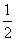 ),M(0,1),N(0,2),点P(x,y)在抛物线x2=2y上。
),M(0,1),N(0,2),点P(x,y)在抛物线x2=2y上。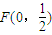 ,M(0,1),N(0,2).点P(x,y)在抛物线x2=2y上
,M(0,1),N(0,2).点P(x,y)在抛物线x2=2y上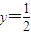 所得的弦长;
所得的弦长;