题目内容
下列说法中:
(1)y=ax+t(t∈R)的图象可以由y=ax的图象平移得到(a>0且a≠1);
(2)y=2x与y=log2x的图象关于y轴对称;
(3)方程log5(2x+1)=log5(x2-2)的解集为1,3;
(4)函数y=ln(1+x)+ln(1-x)为奇函数;正确的是 ________.
解:(1)y=ax+t(t∈R)的图象可以由y=ax的图象平移得到(a>0且a≠1)是正确的;
(2)y=2x与y=log2x互为反函数,互为反函数的两个函数的图象关于y=x对称,故(2)是错误的;
(3)由log5(2x+1)=log5(x2-2)得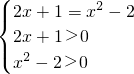 解得x=3,故(3)不对;
解得x=3,故(3)不对;
(4)由函数y=ln(1+x)+ln(1-x)得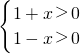 得-1<x<1,故定义域关于原点对称,又f(-x)=ln(1-x)+ln(1+x)=f(x)
得-1<x<1,故定义域关于原点对称,又f(-x)=ln(1-x)+ln(1+x)=f(x)
故函数y=ln(1+x)+ln(1-x)为偶函数,故(4)不对.
故答案为 (1)
分析:(1)考查函数图象的平移规则:左加右减,要注意平移不改变函数的类型;
(2)二个函数互为反函数的关系,由反函数的对称性判断其正误;
(3)解对数方程,一般将对数式转化,尤要注意真数大于0这一隐含条件;
(4)用奇函数的定义来验证,注意验证其定义域关于原点对称这一隐含条件.
点评:本题考点是指数函数图象的变换,考查了函数图象的平移规则,反函数的图象对称性,解对数方程以及函数奇偶性的判断,本题是一个考查函数基本性质的题,属于双基练习题,基本题型,做题时一定要厘清楚其推理规律,建立起相关的完备知识体系.
(2)y=2x与y=log2x互为反函数,互为反函数的两个函数的图象关于y=x对称,故(2)是错误的;
(3)由log5(2x+1)=log5(x2-2)得
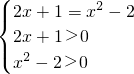 解得x=3,故(3)不对;
解得x=3,故(3)不对;(4)由函数y=ln(1+x)+ln(1-x)得
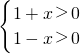 得-1<x<1,故定义域关于原点对称,又f(-x)=ln(1-x)+ln(1+x)=f(x)
得-1<x<1,故定义域关于原点对称,又f(-x)=ln(1-x)+ln(1+x)=f(x)故函数y=ln(1+x)+ln(1-x)为偶函数,故(4)不对.
故答案为 (1)
分析:(1)考查函数图象的平移规则:左加右减,要注意平移不改变函数的类型;
(2)二个函数互为反函数的关系,由反函数的对称性判断其正误;
(3)解对数方程,一般将对数式转化,尤要注意真数大于0这一隐含条件;
(4)用奇函数的定义来验证,注意验证其定义域关于原点对称这一隐含条件.
点评:本题考点是指数函数图象的变换,考查了函数图象的平移规则,反函数的图象对称性,解对数方程以及函数奇偶性的判断,本题是一个考查函数基本性质的题,属于双基练习题,基本题型,做题时一定要厘清楚其推理规律,建立起相关的完备知识体系.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、当n=0时,函数y=xn的图象是一条直线 | B、幂函数的图象都过(0,0)和(1,1) | C、幂函数的图象不可能出现在第三象限 | D、图象不经过(-1,1)的幂函数一定不是偶函数 |