题目内容
函数f(x)=
,则下列说法中正确的是
①函数y=f(x)-ln(x+1)有3个零点;
②若x>0,时,函数f(x)≤
恒成立,则实数k的取值范围是[
,+∞);
③函数f(x)的极大值中一定存在最小值;
④f(x)=2kf(x+2k),(k∈N),对于一切x∈[0,+∞)恒成立.
|
②④
②④
(只写序号)①函数y=f(x)-ln(x+1)有3个零点;
②若x>0,时,函数f(x)≤
| k |
| x |
| 3 |
| 2 |
③函数f(x)的极大值中一定存在最小值;
④f(x)=2kf(x+2k),(k∈N),对于一切x∈[0,+∞)恒成立.
分析:在同一坐标系中画出函数y=f(x)与y=ln(x+1)的图象,判断函数图象的交点的个数,进而可判断①;分析函数f(x)的极大值点坐标中,横纵坐标积最大值,进而可判断②;根据函数f(x)的图象,可判断函数f(x)的极大值无最小值,进而可判断③;利用数学归纳法,可证得f(x)=2kf(x+2k),(k∈N),对于一切x∈[0,+∞)恒成立,进而判断④.
解答:解:f(x)=
的图象如下图所示:
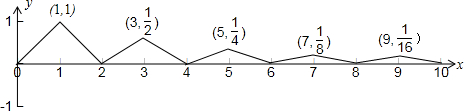
∵函数y=f(x)与y=ln(x+1)的图象只有两个公共点,故函数y=f(x)-ln(x+1)有2个零点,故①错误;
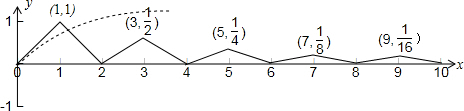
函数f(x)的极大值点坐标中,横纵坐标积最大的为(3,
)点,
若函数f(x)≤
恒成立,则k≥3×
=
,故实数k的取值范围是[
,+∞),故②正确;
函数f(x)的极大值中一定不存在最小值,故③错误;
当k=0时,f(x)=f(x)成立.
假设k=n时,f(x)=2nf(x+2n),(n∈N)成立.
则k=n+1时,
2n+1f[x+2(n+1)]=2n+1f(x+2n+2)=2n+1•
f(x+2n)=2nf(x+2n)=f(x)
即此时f(x)=2kf(x+2k),(k∈N)仍成立,
故f(x)=2kf(x+2k),(k∈N),对于一切x∈[0,+∞)恒成立,故④正确;
故答案为:②④
|

∵函数y=f(x)与y=ln(x+1)的图象只有两个公共点,故函数y=f(x)-ln(x+1)有2个零点,故①错误;

函数f(x)的极大值点坐标中,横纵坐标积最大的为(3,
| 1 |
| 2 |
若函数f(x)≤
| k |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
函数f(x)的极大值中一定不存在最小值,故③错误;
当k=0时,f(x)=f(x)成立.
假设k=n时,f(x)=2nf(x+2n),(n∈N)成立.
则k=n+1时,
2n+1f[x+2(n+1)]=2n+1f(x+2n+2)=2n+1•
| 1 |
| 2 |
即此时f(x)=2kf(x+2k),(k∈N)仍成立,
故f(x)=2kf(x+2k),(k∈N),对于一切x∈[0,+∞)恒成立,故④正确;
故答案为:②④
点评:本题以命题的真假判断为载体考查了函数的零点,函数恒成立问题,函数的极值,是函数图象和性质的综合应用,难度较大,属于难题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目