题目内容
本小题满分12分)
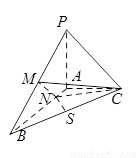
已知三棱锥PABC中,PA⊥平面ABC,AB⊥AC,PA=AC=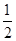 AB,
AB,
N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(I)证明:CM⊥SN;(II)求SN与平面CMN所成角的大小.
【答案】
(1)证明:见解析;(2) SN与平面CMN所成角为45°.
【解析】如果已知向量的坐标,求向量的夹角,我们可以分别求出两个向量的坐标,进一步求出两个向量的模及他们的数量积,然后代入公式cosθ得到。
(1)要证明CM⊥SN,我们可要证明 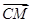 ·
·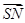 =0即可,根据向量数量积的运算,我们不难证明;
=0即可,根据向量数量积的运算,我们不难证明;
(2)要求SN与平面CMN所成角的大小,我们只要利用求向量夹角的方法,求出SN和方向向量与平面CMN的法向量的夹角,再由它们之间的关系,易求出SN与平面CMN所成角的大小.
解:设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系则P(0,0,1),C(0,1,0),B(2,0,0),M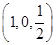 ,N
,N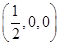 ,S
,S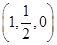 .
.
(1)证明: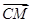 =(1,-1,
=(1,-1,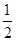 ),
),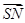 =
=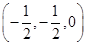 ,因为
,因为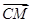 ·
·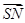 =-
=-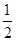 +
+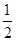 +0=0,
+0=0,
所以CM⊥SN.
(2) 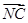 =
=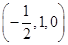 ,设a=(x,y,z)为平面CMN的一个法向量,则
,设a=(x,y,z)为平面CMN的一个法向量,则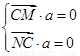 ,
,
∴ ,取x=2,得a=(2,1,-2).因为|cos〈a,
,取x=2,得a=(2,1,-2).因为|cos〈a,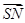 〉|=
〉|=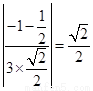 ,
,
所以SN与平面CMN所成角为45°.

练习册系列答案
相关题目