题目内容
在已知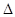 ABC的内角
ABC的内角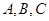 的对边
的对边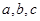 若a=csinA则
若a=csinA则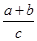 的最大值为( )
的最大值为( )
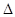 ABC的内角
ABC的内角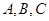 的对边
的对边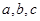 若a=csinA则
若a=csinA则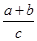 的最大值为( )
的最大值为( )A.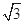 | B.1 | C.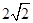 | D.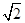 |
D
试题分析:根据正弦定理及a=csinA求得C.进而根据勾股定理可知c2=a2+b2,对
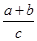 的平方化简整理
的平方化简整理根据基本不等式得到的范围,进而得出答案。解:a=csinA,得到
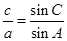 =sinA.所以sinC=1,即C=90°.所以c2=a2+b2.
=sinA.所以sinC=1,即C=90°.所以c2=a2+b2. ,然后根据均值不等式可知结论分母有最小值为2,整个表达式有最大值为2,那么可知
,然后根据均值不等式可知结论分母有最小值为2,整个表达式有最大值为2,那么可知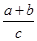 的最大值为
的最大值为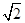 ,选D
,选D点评:本题主要考查正弦定理和基本不等式在解三角形中的应用

练习册系列答案
相关题目
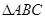 的外接圆半径
的外接圆半径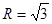 ,角
,角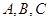 的对边分别是
的对边分别是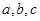 ,且
,且
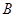 和边长
和边长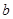 ;
;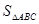 的最大值及取得最大值时的
的最大值及取得最大值时的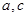 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.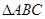 的三个内角
的三个内角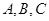 所对的边分别为
所对的边分别为 ,
,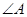 是锐角,且
是锐角,且 .
.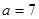 ,
,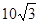 ,求
,求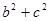 的值.
的值.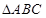 的内角
的内角 所对的边分别为
所对的边分别为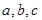 .若
.若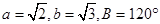 ,则角
,则角 .
. 中,角A,B,C所对的边分别是
中,角A,B,C所对的边分别是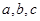 ,且
,且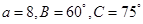 ,
,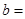 .
. 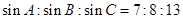 ,求角
,求角 大小
大小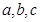 是A,B,C所对的边,S是该三角形的面积,且
是A,B,C所对的边,S是该三角形的面积,且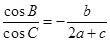
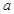 =4,
=4,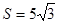 ,求
,求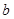 的值。
的值。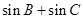 的最大值.
的最大值.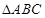 中,边
中,边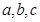 所对的角分别为
所对的角分别为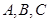 ,
,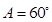 ,
,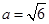 ,
,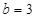 ,则
,则