题目内容
若矩阵A有特征值λ1=2,λ2=-1,它们所对应的特征向量分别为e1= 和e2=
和e2=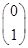 .
.
(1)求矩阵A.
(2)求曲线x2+y2=1在矩阵A的变换下得到的新曲线方程.
 和e2=
和e2=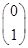 .
.(1)求矩阵A.
(2)求曲线x2+y2=1在矩阵A的变换下得到的新曲线方程.
(1) A=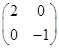 (2)
(2) 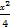 +y2=1
+y2=1
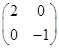 (2)
(2) 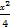 +y2=1
+y2=1(1)设A=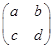 ,由Ae1=λ1e1,Ae2=λ2e2得
,由Ae1=λ1e1,Ae2=λ2e2得
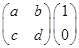 =2
=2 =
=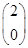 ,
,
 =-1×
=-1×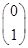 =
=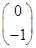 ,
,
∴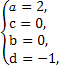 ∴A=
∴A=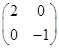 .
.
(2)设曲线x2+y2=1上任意一点(x,y)在矩阵A对应的变换作用下得到的点为(x',y'),
则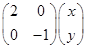 =
=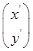 ,即
,即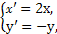
所以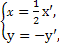 从而(
从而( x')2+(-y')2=1,
x')2+(-y')2=1,
即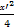 +y'2=1,
+y'2=1,
∴所求新曲线方程为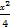 +y2=1.
+y2=1.
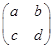 ,由Ae1=λ1e1,Ae2=λ2e2得
,由Ae1=λ1e1,Ae2=λ2e2得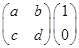 =2
=2 =
=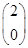 ,
, =-1×
=-1×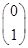 =
=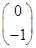 ,
,∴
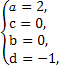 ∴A=
∴A=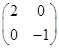 .
.(2)设曲线x2+y2=1上任意一点(x,y)在矩阵A对应的变换作用下得到的点为(x',y'),
则
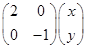 =
=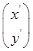 ,即
,即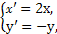
所以
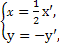 从而(
从而( x')2+(-y')2=1,
x')2+(-y')2=1,即
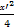 +y'2=1,
+y'2=1,∴所求新曲线方程为
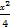 +y2=1.
+y2=1.
练习册系列答案
相关题目
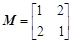 ,
,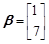 ,计算
,计算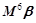 .
.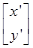 =
=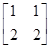
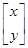 下,直线x+y=k(k为常数)上的所有点都变为一个点,求此点坐标.
下,直线x+y=k(k为常数)上的所有点都变为一个点,求此点坐标. 当
当 时,函数
时,函数 的最小值为-4,则t的取值范围是
的最小值为-4,则t的取值范围是  的逆矩阵.
的逆矩阵.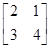 .
.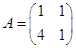 ,则矩阵
,则矩阵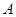 的一个特征值
的一个特征值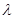 和对应的一个特征向量
和对应的一个特征向量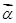 为
为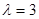 ,
,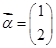
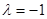 ,
,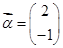
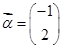
 、
、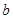 、
、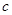 是
是 的三边长,且满足
的三边长,且满足 ,则
,则