Question

【题目】求证： n 棱柱中过侧棱的对角面的个数是 ．

Answer 1

【答案】【解答】
证明：①当 n=4 时，四棱柱有 2 个对角面： ，命题成立．
②假设 n=k （）时，命题成立，即符合条件的棱柱的对角面有 个．
现在考虑 n=k+1 时的情形．
第 k+1 条棱Ak+1Bk+1 与其余和它不相邻的 k-2 条棱分别增加了1个对角共 k-2 个，而面A1B1BkAk 变成了对角面．因此对角面的个数变为： ，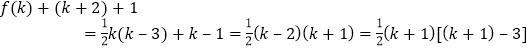
即 成立．
由①和②可知，对任何 ，命题成立．
【解析】本题主要考查了数学归纳法，解决问题的关键是根据所给几何问题分析计算即可
【考点精析】利用数学归纳法的定义对题目进行判断即可得到答案，需要熟知数学归纳法是证明关于正整数n的命题的一种方法．