题目内容
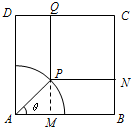 如图边长为2的正方形花园的一角是以A为中心,1为半径的扇形水池.现需在其余部分设计一个矩形草坪PNCQ,其中P是水池边上任意一点,点N、Q分别在边BC和CD上,设∠PAB为θ.
如图边长为2的正方形花园的一角是以A为中心,1为半径的扇形水池.现需在其余部分设计一个矩形草坪PNCQ,其中P是水池边上任意一点,点N、Q分别在边BC和CD上,设∠PAB为θ.(I)用θ表示矩形草坪PNCQ的面积,并求其最小值;
(II)求点P到边BC和AB距离之比
| PN | PM |
分析:(I)先利用∠PAB为θ,|AP|=1?AM=COSθ,PM=sinθ,?矩形草坪PNCQ面积S=(2-cosθ)(2-sinθ),向下整理得[sin(θ+
)-
]2-2+
,再利用二次函数在闭区间上的最值求法即可求矩形草坪PNCQ的面积的最小值;
(II)先求得y=
=
,再求其导函数,利用其导函数研究出原函数在给定区间上的单调性,进而求出其最小值.
| π |
| 4 |
| 2 |
| 7 |
| 2 |
(II)先求得y=
| PN |
| PM |
| 2-cosθ |
| sinθ |
解答:解:(I)因为∠PAB为θ,|AP|=1.
∴AM=COSθ,PM=sinθ,
PN=2-cosθ,PQ=2-sinθ,
∴矩形草坪PNCQ面积S=(2-cosθ)(2-sinθ)
=4-2(sinθ+cosθ)+sinθ•cosθ
=4-2(sinθ+cosθ)+
=
-2
sin(θ+
)+
=sin2(θ+
)-2
sin(θ+
)+
=[sin(θ+
)-
]2-2+
.
∵θ∈[0,
],∴θ+
∈[
,
].sin(θ+
)∈[
,1].
∴当sin(θ+
)=1,即θ=
时,面积有最小值此时s=(1-
)2-2+
=
-2
.
故当θ=
,最小值为
-2
;(6分)
(II)∵y=
=
∴y′=
(0≤θ≤
),令1-2cosθ=0?θ=
.
所以当θ=
时,ymin=
(12分)
∴AM=COSθ,PM=sinθ,
PN=2-cosθ,PQ=2-sinθ,
∴矩形草坪PNCQ面积S=(2-cosθ)(2-sinθ)
=4-2(sinθ+cosθ)+sinθ•cosθ
=4-2(sinθ+cosθ)+
| (sinθ+cosθ)2-1 |
| 2 |
=
| 7 |
| 2 |
| 2 |
| π |
| 4 |
[
| ||||
| 2 |
=sin2(θ+
| π |
| 4 |
| 2 |
| π |
| 4 |
| 7 |
| 2 |
=[sin(θ+
| π |
| 4 |
| 2 |
| 7 |
| 2 |
∵θ∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴当sin(θ+
| π |
| 4 |
| π |
| 4 |
| 2 |
| 7 |
| 2 |
| 9 |
| 2 |
| 2 |
故当θ=
| π |
| 4 |
| 9 |
| 2 |
| 2 |
(II)∵y=
| PN |
| PM |
| 2-cosθ |
| sinθ |
∴y′=
| 1-2cosθ |
| sin2θ |
| π |
| 2 |
| π |
| 3 |
| θ | 0 | (0,
|
|
(
|
| ||||||||||
|
- ↘ |
0 极小 |
+ ↗ |
| π |
| 3 |
| 3 |
点评:本题主要考查利用导数求闭区间上函数的最值,是对二次函数,三角函数等知识的综合考查,属于中档题.

练习册系列答案
相关题目
 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
 如图边长为2的正方形花园的一角是以A为中心,1为半径的扇形水池.现需在其余部分设计一个矩形草坪PNCQ,其中P是水池边上任意一点,点N、Q分别在边BC和CD上,设∠PAB为θ.
如图边长为2的正方形花园的一角是以A为中心,1为半径的扇形水池.现需在其余部分设计一个矩形草坪PNCQ,其中P是水池边上任意一点,点N、Q分别在边BC和CD上,设∠PAB为θ.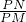 的最小值.
的最小值. 的最小值.
的最小值.