题目内容
(本小题满分12分)![]()
![]()
![]()
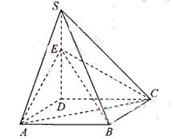
如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=![]() a(0<
a(0<![]() ≦1).
≦1).
(Ⅰ)求证:对任意的![]()
![]() (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求![]() 的值。
的值。
(I)见解析(Ⅱ)![]()
解析:
(Ⅰ)证法1:如图1,连接BE、BD,由地面ABCD是正方形可得AC⊥BD。
![]() SD⊥平面ABCD,
SD⊥平面ABCD,![]() BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,![]() AC⊥BE
AC⊥BE
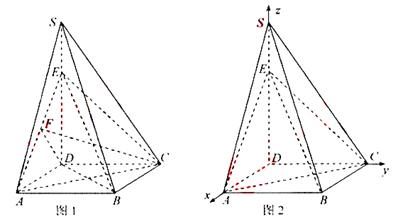
(Ⅱ)解法1:如图1,由SD⊥平面ABCD知,∠DBE= ![]() ,
,
![]() SD⊥平面ABCD,CD
SD⊥平面ABCD,CD![]() 平面ABCD,
平面ABCD, ![]() SD⊥CD。
SD⊥CD。
又底面ABCD是正方形,![]() CD⊥AD,而SD
CD⊥AD,而SD![]() AD=D,CD⊥平面SAD.
AD=D,CD⊥平面SAD.
连接AE、CE,过点D在平面SAD内作DE⊥AE于F,连接CF,则CF⊥AE,
故∠CDF是二面角C-AE-D的平面角,即∠CDF=![]() 。
。
在Rt△BDE中,![]() BD=2a,DE=
BD=2a,DE=![]()
![]()
在Rt△ADE中, ![]()
从而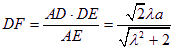
在![]() 中,
中,![]() .
.
由![]() ,得
,得![]()
![]() .
.
由![]() ,解得
,解得![]() ,即为所求.
,即为所求.![]()
![]()
![]()
证法2:以D为原点,![]() 的方向分别作为x,y,z轴的正方向建立如
的方向分别作为x,y,z轴的正方向建立如
图2所示的空间直角坐标系,则
D(0,0,0),A(![]() ,0,0),B(
,0,0),B(![]() ,
,![]() ,0),C(0,
,0),C(0,![]() ,0),E(0,0
,0),E(0,0![]() ),
),
![]()
![]()
![]()
![]() ,
,
即![]() 。
。
解法2:
由(I)得![]() .
.
设平面ACE的法向量为n=(x,y,z),则由![]() 得
得
![]()
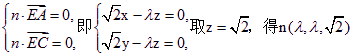 。
。
![]() 易知平面ABCD与平面ADE的一个法向量分别为
易知平面ABCD与平面ADE的一个法向量分别为![]() .
.
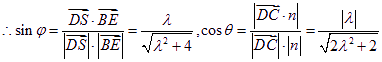 .
.
![]() 0<
0<![]() ,
,![]() ,
,
![]() .
.
由于![]() ,解得
,解得![]() ,即为所求。
,即为所求。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目