��Ŀ����
������ԭ�㣬������x���ϵ�������C����P��4��4�������������߽���F��ֱ�߽���������A��B���㣬��M��N�ֱ�ΪA��B��������������l�ϵ���Ӱ����l��x��Ľ���ΪE����1����������C�ı����̣�
��2��ijѧϰС���ڼ������̬��ѧ�����İ����£��õ��˹���������C���ʵ����²��룺��ֱ��AN��BM���ཻ��ԭ��O������֤���ý�������ȷ�ģ�
��3����С�麢���о�������C�С�AEB�Ĵ�С��Χ����ͨ������
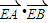 �Ľ��������һ������Ϊ��ȷ�����AEB�йص����ۣ���˵�����ɣ�
�Ľ��������һ������Ϊ��ȷ�����AEB�йص����ۣ���˵�����ɣ�
���𰸡���������1��������ɿ��������ߵķ���y2=2px��p��0����������C����P��4��4������p���������������߷���
��2����֤�� x1��x2ʱ��kOA=kON��˵��A��O��N���㹲�ߣ��� x1=x2ʱ�����ѵõ�ABNMΪ���Σ����жԳ��Կ�֪��OΪ�Խ���AN��BM�Ľ��㣬���Դ�ʱA��O��N���㹲�ߣ�
��3����A��x1��y1����B��x2��y2������ΪAB������F��F��1��0������ x1��x2ʱ��AB���ڵ�ֱ�ߵķ���y=k��x-1����k��0�����������߷��̣���Ϸ��̵ĸ���ϵ����ϵ���� x1=x2ʱ��AB���ڵ�ֱ�ߴ�ֱ��x�ᣬ�������AF=EF=EB=2���ʴ�ʱ��AEB=90°
����⣺��1��������ɿ��������ߵķ���y2=2px��p��0��
��������C����P��4��4����p=2
��y2=4x
��2���� x1��x2ʱ��kOA=kON�����Դ�ʱA��O��N���㹲�ߣ��� x1=x2ʱ�����ѵõ�ABNMΪ���Σ����жԳ��Կ�֪��OΪ�Խ���AN��BM�Ľ��㣬���Դ�ʱA��O��N���㹲�ߣ�
��3����A��x1��y1����B��x2��y2������ΪAB������F��F��1��0����
�� x1��x2ʱ��AB���ڵ�ֱ�ߵķ���y=k��x-1����k��0�����������߷��̿ɵ�k2x2-��2k2+4��x+k2=0��
����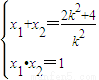
�� x1=x2ʱ��AB���ڵ�ֱ�ߴ�ֱ��x�ᣬ�������AF=EF=EB=2���ʴ�ʱ��AEB=90°
���ϣ���������ۡ���AEBֻ������ǻ�ֱ�ǡ�
������������Ҫ�������������ߵ�������������ߵķ��̣�ֱ���������ߵ�λ�ù�ϵ��Ӧ�ã����̵ĸ���ϵ����ϵ��Ӧ�ã������ۺ������⣮
��2����֤�� x1��x2ʱ��kOA=kON��˵��A��O��N���㹲�ߣ��� x1=x2ʱ�����ѵõ�ABNMΪ���Σ����жԳ��Կ�֪��OΪ�Խ���AN��BM�Ľ��㣬���Դ�ʱA��O��N���㹲�ߣ�
��3����A��x1��y1����B��x2��y2������ΪAB������F��F��1��0������ x1��x2ʱ��AB���ڵ�ֱ�ߵķ���y=k��x-1����k��0�����������߷��̣���Ϸ��̵ĸ���ϵ����ϵ���� x1=x2ʱ��AB���ڵ�ֱ�ߴ�ֱ��x�ᣬ�������AF=EF=EB=2���ʴ�ʱ��AEB=90°
����⣺��1��������ɿ��������ߵķ���y2=2px��p��0��
��������C����P��4��4����p=2
��y2=4x
��2���� x1��x2ʱ��kOA=kON�����Դ�ʱA��O��N���㹲�ߣ��� x1=x2ʱ�����ѵõ�ABNMΪ���Σ����жԳ��Կ�֪��OΪ�Խ���AN��BM�Ľ��㣬���Դ�ʱA��O��N���㹲�ߣ�
��3����A��x1��y1����B��x2��y2������ΪAB������F��F��1��0����
�� x1��x2ʱ��AB���ڵ�ֱ�ߵķ���y=k��x-1����k��0�����������߷��̿ɵ�k2x2-��2k2+4��x+k2=0��
����
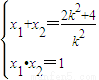
�� x1=x2ʱ��AB���ڵ�ֱ�ߴ�ֱ��x�ᣬ�������AF=EF=EB=2���ʴ�ʱ��AEB=90°
���ϣ���������ۡ���AEBֻ������ǻ�ֱ�ǡ�
������������Ҫ�������������ߵ�������������ߵķ��̣�ֱ���������ߵ�λ�ù�ϵ��Ӧ�ã����̵ĸ���ϵ����ϵ��Ӧ�ã������ۺ������⣮

��ϰ��ϵ�д�
 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
�����Ŀ
������ԭ�㡢������x���ϵ������߱�ֱ��y=x+1�صõ��ҳ���
���������ߵķ����ǣ�������
| 10 |
| A��y2=-x��y2=5x |
| B��y2=-x |
| C��y2=x��y2=-5x |
| D��y2=5x |
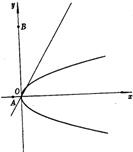 ��ֱ֪��l������ԭ�㣬������C������ԭ�㣬������x���������ϣ�����A��-1��0���͵�B��0��8������l�ĶԳƵ㶼��C�ϣ���ֱ��l��������C�ķ��̣�
��ֱ֪��l������ԭ�㣬������C������ԭ�㣬������x���������ϣ�����A��-1��0���͵�B��0��8������l�ĶԳƵ㶼��C�ϣ���ֱ��l��������C�ķ��̣�