题目内容
一个各条棱都相等的四面体,其外接球半径R,则此四面体的棱长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
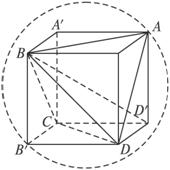
分析:由题意可知,正四面体的外接球,就是以正四面体的棱为面对角线的正方体的外接球,球的直径就是正方体的对角线的长,然后求出正方体的棱长,再求正四面体的棱长即可.
解答:解:正四面体的外接球,就是以正四面体的棱为面对角线的正方体的外接球,
球的直径就是正方体的对角线的长,所以正方体的对角线为2R,
设正方体的棱长为a,所以
a=2R,a=
所以四面体的棱长为:
a=
R
故选C.
球的直径就是正方体的对角线的长,所以正方体的对角线为2R,
设正方体的棱长为a,所以
| 3 |
2
| ||
| 3 |
所以四面体的棱长为:
| 2 |
2
| ||
| 3 |
故选C.
点评:本题考查球的内接多面体的问题,考查空间想象能力,逻辑思维能力,考查计算能力,转化思想,是中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目