Question

甲烷分子(CH₄)由一个碳原子和四个氢原子组成,其空间构型为一个各条棱都相等的四面体,其中四个氢原子分别位于该四面体的四个顶点上,碳原子位于该四面体的中心,它与每个氢原子的距离都相等,若视氢原子、碳原子为一个点,四面体的棱长为a,求碳原子到各个氢原子的距离.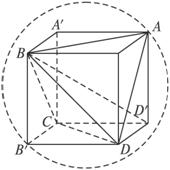

Answer 1

思路分析：由题意立即联想到正四面体的外接球,而正四面体又可以看作是正方体的六条面对角线围成的图形,因此,将正四面体补成一个正方体,从而建立相关量之间的关系.

解:显然,四面体的四个顶点在以中心(碳原子)为球心,中心到各顶点(氢原子)的距离为半径的球面上,如图,将此正四面体ABCD补成正方体BD′,其中A′、B′、D′也在球面上,设碳原子到每个氢原子的距离为x,则2x=BD′.

    BD′、AB(a)、AA′之间的关系是a=AB=AA′,2x=BD′=AA′,

    因此x=3·,∴x=a,即碳原子到各个氢原子的距离为a.

讲评:在立体几何中,我们常常将四面体补成正四面体或平行六面体、正四面体补成正方体、过同一个顶点的三条棱两两垂直的四面体补成长方体、四棱锥补成平行六面体,等等,掌握这些补形规律,有助于提高解题能力.