题目内容
已知方向向量为 的直线l过点
的直线l过点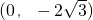 和椭圆
和椭圆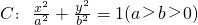 的右焦点,且椭圆的离心率为
的右焦点,且椭圆的离心率为 .
.
(1)求椭圆C的方程:
(2)若已知点M,N是椭圆C上不重合的两点,点D(3,0)满足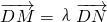 ,求实数λ的取值范围.
,求实数λ的取值范围.
解:(1)因为直线l的方向向量为 所以直线斜率为k=
所以直线斜率为k= ,
,
又因为直线过点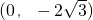
所以直线方程为y+2 =
= x
x
因为a>b,所以椭圆的右焦点为直线与轴的交点,∴椭圆的右焦点为(2,0),所以c=2
∵e= =
= ,∴a=
,∴a= ,∴b2=a2-c2=2
,∴b2=a2-c2=2
∴椭圆方程为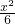 +
+ =1
=1
(2)由已知设直线MN的方程为x=my+3,
由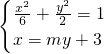 ?(m2+3)y2+6my+3=0,设M.N坐标分别为(x1,y1)(x2,y2)
?(m2+3)y2+6my+3=0,设M.N坐标分别为(x1,y1)(x2,y2)
则y1+y2=-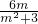 ①y1y2=
①y1y2=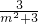 ②
②
△=36m2-12(m2+3)>0?m2>
∵ =(x1-3,y1),
=(x1-3,y1), =(x2-3,y2),
=(x2-3,y2),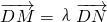 ,显然λ>0且λ≠1
,显然λ>0且λ≠1
∴(x1-3,y1)=λ(x2-3,y2)∴y1=λy2,
代入①②得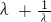 =
=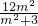 -2=10-
-2=10-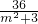 ,
,
∵m2> ?2<
?2<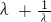 <10?
<10?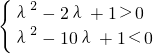
解得5-2 <λ<5+2
<λ<5+2 且λ≠1
且λ≠1
分析:(1)先利用条件求出直线l的方程,找出椭圆的右焦点坐标,再利用椭圆的离心率为 ,就可求出椭圆C的方程:
,就可求出椭圆C的方程:
(2)把直线MN的方程与椭圆方程联立找到关于点M,N纵坐标的方程,再利用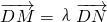 所给出的点M,N纵坐标之间的关系,二者联立借助与判别式大于0就可求实数λ的取值范围.
所给出的点M,N纵坐标之间的关系,二者联立借助与判别式大于0就可求实数λ的取值范围.
点评:本题综合考查了直线与椭圆的位置关系以及向量共线问题.还涉及到直线的方程与斜率,考查运算能力与思维能力、综合分析问题的能力.
 所以直线斜率为k=
所以直线斜率为k= ,
,又因为直线过点
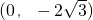
所以直线方程为y+2
 =
= x
x因为a>b,所以椭圆的右焦点为直线与轴的交点,∴椭圆的右焦点为(2,0),所以c=2
∵e=
 =
= ,∴a=
,∴a= ,∴b2=a2-c2=2
,∴b2=a2-c2=2∴椭圆方程为
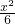 +
+ =1
=1(2)由已知设直线MN的方程为x=my+3,
由
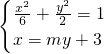 ?(m2+3)y2+6my+3=0,设M.N坐标分别为(x1,y1)(x2,y2)
?(m2+3)y2+6my+3=0,设M.N坐标分别为(x1,y1)(x2,y2)则y1+y2=-
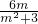 ①y1y2=
①y1y2=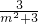 ②
②△=36m2-12(m2+3)>0?m2>

∵
 =(x1-3,y1),
=(x1-3,y1), =(x2-3,y2),
=(x2-3,y2),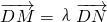 ,显然λ>0且λ≠1
,显然λ>0且λ≠1∴(x1-3,y1)=λ(x2-3,y2)∴y1=λy2,
代入①②得
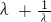 =
=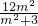 -2=10-
-2=10-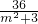 ,
,∵m2>
 ?2<
?2<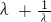 <10?
<10?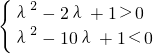
解得5-2
 <λ<5+2
<λ<5+2 且λ≠1
且λ≠1分析:(1)先利用条件求出直线l的方程,找出椭圆的右焦点坐标,再利用椭圆的离心率为
 ,就可求出椭圆C的方程:
,就可求出椭圆C的方程:(2)把直线MN的方程与椭圆方程联立找到关于点M,N纵坐标的方程,再利用
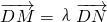 所给出的点M,N纵坐标之间的关系,二者联立借助与判别式大于0就可求实数λ的取值范围.
所给出的点M,N纵坐标之间的关系,二者联立借助与判别式大于0就可求实数λ的取值范围.点评:本题综合考查了直线与椭圆的位置关系以及向量共线问题.还涉及到直线的方程与斜率,考查运算能力与思维能力、综合分析问题的能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
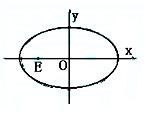

 的直线l过椭圆
的直线l过椭圆 的焦点以及点(0,
的焦点以及点(0, ),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为 。
。 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程