ΧβΡΩΡΎ»ί
Θ®05ΡξΗΘΫ®ΨμΘ©Θ®12Ζ÷Θ©
“―÷ΣΖΫœρœρΝΩΈΣ![]() ΒΡ÷±œΏlΙΐΒψΘ®0Θ§Θ≠2
ΒΡ÷±œΏlΙΐΒψΘ®0Θ§Θ≠2![]() Θ©ΚΆΆ÷‘≤CΘΚ
Θ©ΚΆΆ÷‘≤CΘΚ![]() ΒΡΫΙΒψΘ§«“Ά÷‘≤CΒΡ÷––ΡΙΊ”Ύ÷±œΏlΒΡΕ‘≥ΤΒψ‘ΎΆ÷‘≤CΒΡ”“ΉΦœΏ…œ.
ΒΡΫΙΒψΘ§«“Ά÷‘≤CΒΡ÷––ΡΙΊ”Ύ÷±œΏlΒΡΕ‘≥ΤΒψ‘ΎΆ÷‘≤CΒΡ”“ΉΦœΏ…œ.
Θ®ΔώΘ©«σΆ÷‘≤CΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ© «Ζώ¥φ‘ΎΙΐΒψEΘ®Θ≠2Θ§0Θ©ΒΡ÷±œΏmΫΜΆ÷‘≤C”ΎΒψMΓΔNΘ§¬ζΉψ![]() Θ§
Θ§
cotΓœMONΓΌ0Θ®OΈΣ‘≠ΒψΘ©.»τ¥φ‘ΎΘ§«σ÷±œΏmΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
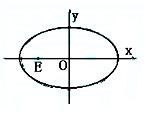
ΫβΈωΘΚ(Δώ)”…Χβ“βΩ…ΒΟ÷±œΏΠ…ΘΚ![]() , ΔΌ
, ΔΌ
Ιΐ‘≠Βψ¥Ι÷±Π…ΒΡΖΫ≥ΧΈΣ![]() ΔΎ
ΔΎ
ΫβΔΌΔΎΒΟx=![]() .ΓΏΆ÷‘≤÷––ΡO(0,0)ΙΊ”Ύ÷±œΏΠ…ΒΡΕ‘≥ΤΒψ‘ΎΆ÷‘≤CΒΡ”“ΉΦœΏ…œ,
.ΓΏΆ÷‘≤÷––ΡO(0,0)ΙΊ”Ύ÷±œΏΠ…ΒΡΕ‘≥ΤΒψ‘ΎΆ÷‘≤CΒΡ”“ΉΦœΏ…œ,
Γύ![]() .ΓΏ÷±œΏΠ…ΙΐΆ÷‘≤ΫΙΒψ,ΓύΗΟΫΙΒψΉχ±ξΈΣ(2,0).
.ΓΏ÷±œΏΠ…ΙΐΆ÷‘≤ΫΙΒψ,ΓύΗΟΫΙΒψΉχ±ξΈΣ(2,0).
Γύa2=6,c=2,b2=2,Ι Ά÷‘≤CΒΡΖΫ≥ΧΈΣ![]() . Δέ
. Δέ
(Δρ)…ηM(x1,y1),N(x2,y2),Β±÷±œΏm≤Μ¥Ι÷±x÷α ±,÷±œΏmΘΚy=k(x+2)¥ζ»κΔέ,’ϊάμΒΟ
(3k2+1)x2+12k2x+12k2-6=0,‘ρx1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
|MN|=![]()
ΒψOΒΫ÷±œΏMNΒΡΨύάκd=![]() .ΓΏ
.ΓΏ![]() cotΓœMON,Φ¥
cotΓœMON,Φ¥
![]() ,
,
Γύ![]() ,Γύ
,Γύ![]() ,
,
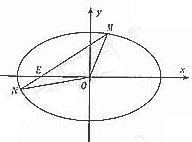
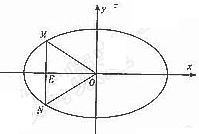
Φ¥![]() .’ϊάμΒΟ
.’ϊάμΒΟ![]() .
.
Β±÷±œΏm¥Ι÷±x÷α ±,“≤¬ζΉψ![]()
Ι ÷±œΏmΒΡΖΫ≥ΧΈΣ![]() Μρy=
Μρy=![]() Μρx=-2.
Μρx=-2.
Ψ≠Φλ―ι…œ ω÷±œΏΨυ¬ζΉψ![]() .
.
Υυ‘ΎΥυ«σ÷±œΏΖΫ≥ΧΈΣ![]() Μρy=
Μρy=![]() Μρx=-2..
Μρx=-2..

 ΩΎΥψΧβΧλΧλΝΖœΒΝ–¥πΑΗ
ΩΎΥψΧβΧλΧλΝΖœΒΝ–¥πΑΗ