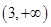题目内容
函数f(x)=lg(x2-3x)的单调递增区间是 .
(3,+∞)
试题分析:函数
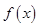 定义域
定义域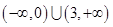 ,
,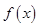 函数看作由
函数看作由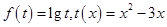 复合而成,
复合而成,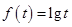 在定义域内是增函数,
在定义域内是增函数,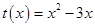 在
在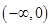 上是减函数,在
上是减函数,在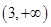 上是增函数,所以原函数的增区间为
上是增函数,所以原函数的增区间为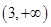
点评:符合函数的单调性是由构成复合函数的两个基本初等函数单调性共同决定,当两函数单调性相同时,复合后递增,当两函数单调性相反时,复合后递减

练习册系列答案
相关题目
题目内容
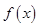 定义域
定义域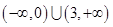 ,
,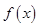 函数看作由
函数看作由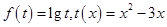 复合而成,
复合而成,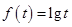 在定义域内是增函数,
在定义域内是增函数,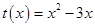 在
在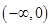 上是减函数,在
上是减函数,在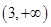 上是增函数,所以原函数的增区间为
上是增函数,所以原函数的增区间为