题目内容
函数 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:
①若P∩M= ,则f(P)∩f(M)=
,则f(P)∩f(M)= ;
;
②若P∩M≠ ,则f(P)∩f(M) ≠
,则f(P)∩f(M) ≠ ;
;
③若P∪M=R,则f(P)∪f(M)=R;
④若P∪M≠R,则f(P)∪f(M)≠R.
其中正确判断有( )
A 0个 B 1个 C 2个 D 4个
A
解析试题分析:函数的表达式知,可借助两个函数y=x与y=-x图象来研究,分析可得答案.
由题意知函数f(P)、f(M)的图象如图所示.
设
故①错误
同理可知当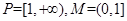 ,②不正确.
,②不正确.
设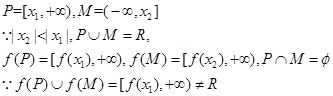
,故③错误.
④若 则
则 .这是不对的 若P={非负实数},M={正实数}
.这是不对的 若P={非负实数},M={正实数}
则f(P)={非负实数},f(M)={负实数}
则f(P)∪f(M)=R.故④错,故选A
考点:本试题主要是考查了同学们对于与集合,函数相关的创新试题的分析,和解决问题能力的运用,是中档题。
点评:考查对题设条件的理解与转化能力,本题中题设条件颇多,审题费时,需仔细审题才能把握其脉络,故研究时借用两个函数的图象,借助图形的直观来来帮助判断命题的正误,以形助数,是解决数学问题常用的一种思路。

已知函数 对任意
对任意 都有
都有 ,若
,若 的图象关于直线
的图象关于直线 对称,且
对称,且 ,则
,则
| A.2 | B.3 | C.4 | D.0 |
函数 的零点所在的大致区间是
的零点所在的大致区间是
| A.(6,7) | B.(7,8) | C.(8,9) | D.(9,10) |
函数 的值域为( )
的值域为( )
A. | B. | C. | D. |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D. |
函数 的定义域是( )
的定义域是( )
| A. (1,2) | B. [1,4] | C. [1,2) | D. (1,2] |
已知 ,若函数
,若函数 ,则
,则 的
的
根的个数最多有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
定义在 上的函数
上的函数 ,如果存在函数
,如果存在函数 ,使得
,使得 对一切实数
对一切实数 都成立,则称
都成立,则称 是函数
是函数 的一个“亲密函数”,现有如下的命题:
的一个“亲密函数”,现有如下的命题:
(1)对于给定的函数 ,其“亲密函数”有可能不存在,也可能有无数个;
,其“亲密函数”有可能不存在,也可能有无数个;
(2) 是
是 的一个“亲密函数”;
的一个“亲密函数”;
(3)定义域与值域都是 的函数
的函数 不存在“亲密函数”。
不存在“亲密函数”。
其中正确的命题是( )
| A.(1) | B.(2) | C.(1)(2) | D.(1)(3) |
已知以 为周期的函数
为周期的函数 ,其中
,其中 。若方程
。若方程 恰有5个实数解,则
恰有5个实数解,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |