题目内容
【题目】各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() .各项均为正数的等比数列
.各项均为正数的等比数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() .
.
①求![]() ;
;
②若对任意![]() ,
,![]() ,均有
,均有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)令![]() 可求得
可求得![]() ,再令
,再令![]() ,由
,由![]() 得
得![]() ,两式作差并结合已知条件得出
,两式作差并结合已知条件得出![]() ,结合
,结合![]() 可知数列
可知数列![]() 是等差数列,确定数列
是等差数列,确定数列![]() 的首项和公差,可求得
的首项和公差,可求得![]() ,并根据已知条件求出等比数列
,并根据已知条件求出等比数列![]() 的首项和公比,由此可求得
的首项和公比,由此可求得![]() ;
;
(2)①求得![]() ,利用错位相减法可求得
,利用错位相减法可求得![]() ;
;
②由题意可得![]() 对任意的
对任意的![]() 且
且![]() 恒成立,由参变量分离法得
恒成立,由参变量分离法得![]() ,构造数列
,构造数列![]() ,利用定义判断数列
,利用定义判断数列![]() 的单调性,求得数列
的单调性,求得数列![]() 的最大项,由此可得出实数
的最大项,由此可得出实数![]() 的取值范围.
的取值范围.
(1)对任意的![]() ,
,![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,由
时,由![]() 得
得![]() ,
,
两式作差得![]() ,即
,即![]() ,
,
又因为数列![]() 各项均为正数,则
各项均为正数,则![]() ,所以,
,所以,![]() ,
,
又![]() ,所以,数列
,所以,数列![]() 是等差数列,且首项为
是等差数列,且首项为![]() ,公差为
,公差为![]() ,
,
![]() .
.
设等比数列![]() 的公比为
的公比为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ;
;
(2)①![]() ,
,![]() ,
,
![]() ,
,
上述两式作差得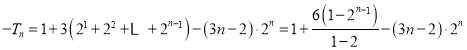
![]() ,
,
因此,![]() ;
;
②由题意可知![]() 对任意的
对任意的![]() 且
且![]() 恒成立,
恒成立,
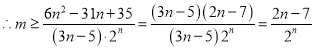 ,即
,即![]() 恒成立,
恒成立,
设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,此时数列
,此时数列![]() 单调递增,即
单调递增,即![]() ;
;
当![]() 时,
时,![]() ,此时数列
,此时数列![]() 单调递减,即
单调递减,即![]() .
.
所以,数列![]() 中最大项为
中最大项为![]() ,
,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】现从某医院中随机抽取了七位医护人员的关爱患者考核分数(患者考核: ![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:
表示;医护专业知识考核分数(试卷考试: ![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到
的线性回归方程(计算结果精确到![]() );
);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为![]() 分时,他的关爱患者考核分数(精确到
分时,他的关爱患者考核分数(精确到![]() );
);
(3)现要从医护专业知识考核分数![]() 分以下的医护人员中选派
分以下的医护人员中选派![]() 人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在
人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在![]() 分以下的概率.
分以下的概率.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为 ,
, ![]() .
.
【题目】某学校为鼓励家校互动,与某手机通讯商合作,为教师办理流量套餐.为了解该校教师手机流量使用情况,通过抽样,得到![]() 位教师近
位教师近![]() 年每人手机月平均使用流量
年每人手机月平均使用流量![]() (单位:
(单位:![]() )的数据,其频率分布直方图如下:
)的数据,其频率分布直方图如下:

若将每位教师的手机月平均使用流量分别视为其手机月使用流量,并将频率为概率,回答以下问题.
(Ⅰ) 从该校教师中随机抽取![]() 人,求这
人,求这![]() 人中至多有
人中至多有![]() 人月使用流量不超过
人月使用流量不超过![]()
![]() 的概率;
的概率;
(Ⅱ) 现该通讯商推出三款流量套餐,详情如下:
套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位: |
|
|
|
|
|
|
|
|
|
这三款套餐都有如下附加条款:套餐费月初一次性收取,手机使用一旦超出套餐流量,系统就自动帮用户充值![]()
![]() 流量,资费
流量,资费![]() 元;如果又超出充值流量,系统就再次自动帮用户充值
元;如果又超出充值流量,系统就再次自动帮用户充值![]()
![]() 流量,资费
流量,资费![]() 元/次,依次类推,如果当月流量有剩余,系统将自动清零,无法转入次月使用.
元/次,依次类推,如果当月流量有剩余,系统将自动清零,无法转入次月使用.
学校欲订购其中一款流量套餐,为教师支付月套餐费,并承担系统自动充值的流量资费的![]() ,其余部分由教师个人承担,问学校订购哪一款套餐最经济?说明理由.
,其余部分由教师个人承担,问学校订购哪一款套餐最经济?说明理由.