题目内容
已知二次函数f(x)=x2+ax(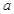
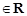 ).
).
(1)若函数y=f(sinx+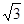 cosx)(
cosx)(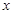
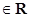 )的最大值为
)的最大值为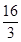 ,求f(x)的最小值;
,求f(x)的最小值;
(2)当a>2时,求证:f(sin2xlog2sin2x+cos2xlog2cos2x)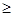 1–a.其中x∈R,x¹kp且x¹kp
1–a.其中x∈R,x¹kp且x¹kp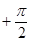 (k∈Z).
(k∈Z).
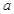
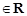 ).
).(1)若函数y=f(sinx+
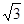 cosx)(
cosx)(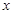
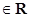 )的最大值为
)的最大值为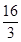 ,求f(x)的最小值;
,求f(x)的最小值;(2)当a>2时,求证:f(sin2xlog2sin2x+cos2xlog2cos2x)
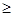 1–a.其中x∈R,x¹kp且x¹kp
1–a.其中x∈R,x¹kp且x¹kp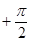 (k∈Z).
(k∈Z).(1)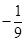 ;(2)见解析.
;(2)见解析.
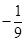 ;(2)见解析.
;(2)见解析.试题分析:(1)先求
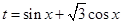 的值域,再讨论a的范围,根据最大值,求最小值;(2)利用导数先求sin2xlog2sin2x+cos2xlog2cos2x的值域,再根据二次函数求结论.
的值域,再讨论a的范围,根据最大值,求最小值;(2)利用导数先求sin2xlog2sin2x+cos2xlog2cos2x的值域,再根据二次函数求结论.试题解析:(1)令
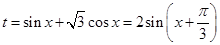 ,
,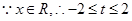 , 2分
, 2分 ,当a<0时,t=–2时,
,当a<0时,t=–2时,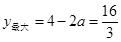 ,
,解得:
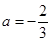
此时
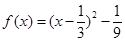 ,
,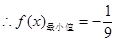 . 2分
. 2分当
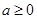 时,t=2时,
时,t=2时,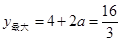 ,解得:
,解得: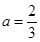
此时,
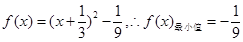
综合上述,条件满足时,
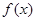 的最小值为
的最小值为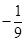 2分
2分(2)
 x∈R,
x∈R,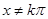 且
且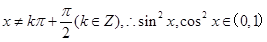
又
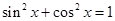 ,故设
,故设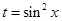 ,则有
,则有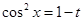
设
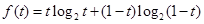 (其中t∈(0,1)) 2分
(其中t∈(0,1)) 2分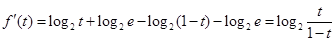 2分
2分令
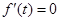 ,得
,得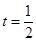
当
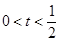 时,
时,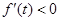 ,所以
,所以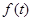 在(0,
在(0,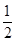 )单调递减,
)单调递减,当
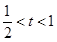 时,
时,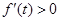 ,所以
,所以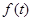 在(
在(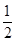 ,1)单调递增,
,1)单调递增, 时
时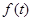 取最小值等于
取最小值等于
即有
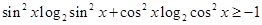 3分
3分当a>2时,
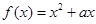 的对称轴
的对称轴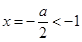 ,
, 上单调递增,
上单调递增,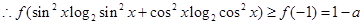 2分
2分
练习册系列答案
相关题目
 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9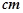 和15
和15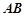 的顶部
的顶部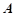 看建筑物
看建筑物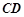 的视角
的视角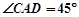 .
.
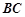 的长度;
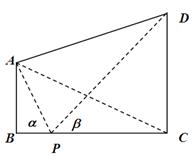
的长度;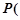 点
点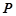 与点
与点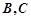 不重合),从点
不重合),从点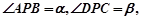 问点
问点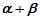 最小?
最小?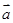 =(2cos
=(2cos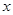 ,1),
,1),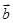 =(cos
=(cos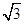 sin2
sin2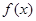 =
=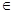 R.
R.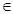 [
[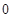 ,
,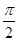 ],求
],求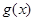 =
=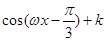 (
(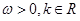 )与
)与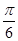 ,2),求函数
,2),求函数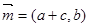 ,
,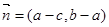 ,且
,且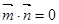 ,其中A、B、C是
,其中A、B、C是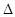 ABC的内角,
ABC的内角,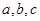 分别是角A,B,C的对边。
分别是角A,B,C的对边。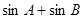 的取值范围;
的取值范围; ,
, ,则
,则 = .
= .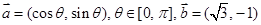 .若
.若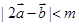 恒成立则实数
恒成立则实数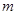 的取值范围是 ( )
的取值范围是 ( )



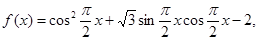 则函数
则函数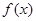 在[-1,1]上的单调增区间为( )
在[-1,1]上的单调增区间为( )



 ,
, ,则
,则 的值为________.
的值为________.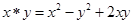 ,则
,则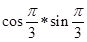 的值是( )
的值是( )


