题目内容
过点A（1，1）且与直线3x+y-1=0平行的直线的方程为（ ）
| A、3x+y-4=0 | B、3x-y-2=0 | C、x+3y-4=0 | D、x-3y+2=0 |
分析：由题意，设所求直线方程为3x+y+c=0，把点A坐标代入求出c，即得所求．
解答：解：∵所求直线与直线3x+y-1=0平行，
∴设所求的直线方程为3x+y+c=0，
又直线过点A（1，1），
∴3×1+1+c=0，
∴c=-4，
∴所求的直线方程为3x+y-4=0；
故选：A．
∴设所求的直线方程为3x+y+c=0，
又直线过点A（1，1），
∴3×1+1+c=0，
∴c=-4，
∴所求的直线方程为3x+y-4=0；
故选：A．
点评：本题考查了求与已知直线平行的直线方程问题，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，
]
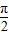，π）
]∪[
，π）
]∪[
]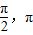