题目内容
设f(x)=(
)x-log2x，已知0＜a＜b＜c，且f（a）•f（b）•f（c）＜0，若x0是函数f（x）的一个零点，那么下列不等式中不可能成立的是（ ）
| 1 |
| 2 |
分析：利用函数与方程之间的关系，结合根的存在性定理进行判断即可．
解答：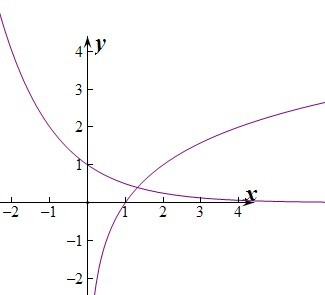
解：由f(x)=(
)x-log2x=0，得(
)x=log2x，设函数y=(
)x，y=log?2x，分别作出函数的图象如图：
因为x0是函数f（x）的一个零点，
由图象可知，当x＜x0时，f（x）＞0，
当x＞x0时，f（x）＜0．
因为0＜a＜b＜c，且f（a）•f（b）•f（c）＜0，
所以f（a）＞0，f（b）＞0，f（c）＜0，
所以由根的存在性定理可知，a＜x0＜b不成立．
故选B．
解：由f(x)=(| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为x0是函数f（x）的一个零点，
由图象可知，当x＜x0时，f（x）＞0，
当x＞x0时，f（x）＜0．
因为0＜a＜b＜c，且f（a）•f（b）•f（c）＜0，
所以f（a）＞0，f（b）＞0，f（c）＜0，
所以由根的存在性定理可知，a＜x0＜b不成立．
故选B．
点评：本题主要考查函数与方程的关系，利用根的存在性定理是解决本题的关键．
练习册系列答案
相关题目
设f(x)=(
)x-x+1，用二分法求方程(
)x-x+1=0在（1，3）内近似解的过程中，f（1）＞0，f（1.5）＜0，f（2）＜0，f（3）＜0，则方程的根落在区间（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、（1，1.5） |
| B、（1.5，2） |
| C、（2，3） |
| D、无法确定 |
设f(x)=(
)x-x+1，用二分法求方程(
)x-x+1=0在（1，3）内近似解的过程中，f（1）＞0，f（1.25）＞0，f（1.5）＜0，f（2）＜0，f（3）＜0，则方程的根落在区间（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、（1，1.25） |
| B、（1.25，1.5） |
| C、（1.5，2） |
| D、（2，3） |