题目内容
（本小题满分12分）
已知
的三个内角
所对的边分别为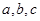
，向量
，
，且
．
(1)求
的大小；
(2)现在给出下列三个条件：①
；②
；③
，试从中再选择两个条件以确定，求出所确定的的面积．
【答案】
（1）
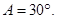（2）面积为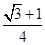
【解析】
试题分析：因为
，
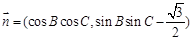，且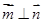
，
所以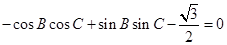
， ……2分
即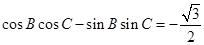
，所以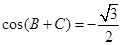
， ……4分
因为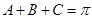
,所以
所以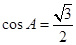
，
因为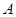
是三角形的内角，所以 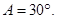……6分
(Ⅱ)方案一:选择①②，可确定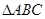
，
因为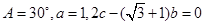
由余弦定理，得：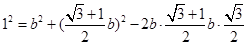
，
整理得：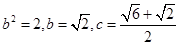
，
……10分
所以
。
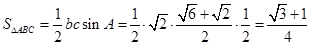……13分
方案二:选择①③，可确定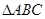，因为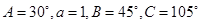
，
又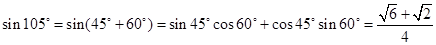
，
由正弦定理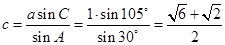
，
……10分
所以
.
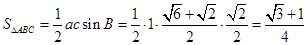……13分
考点：本小题主要考查平面向量的数量积、两角和与差的余弦公式、正弦定理及三角形面积公式的综合应用，考查学生的运算求解能力.
点评：在高考中经常遇到平面向量和三角函数结合的题目，此类问题一般难度不大，灵活选用公式，正确计算即可.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
