题目内容
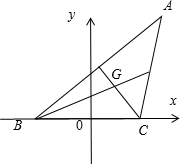
(理科做):已知:如图,△ABC的边BC长为16,AC、AB边上中线长的和为30.
求:(I)△ABC的重心G的轨迹;
(II)顶点A的轨迹方程.
求:(I)△ABC的重心G的轨迹;
(II)顶点A的轨迹方程.
分析:(I)设重心G点坐标为(x,y),以BC所在的直线为X轴,BC中点为原点建立直角坐标系.根据重心分中线比为2:1可知|GC|+|GB|=30×
根据椭圆的定义可知G点的轨迹是以B,C为焦点的椭圆,且除去轴上两点.进而求得椭圆的a,c和b得到G的轨迹方程;
(II)设A点坐标为(u,v),根据重心分中线比为2:1,可得x与u,y与v的关系,代入G的轨迹方程进而可得A的轨迹方程.
| 2 |
| 3 |
(II)设A点坐标为(u,v),根据重心分中线比为2:1,可得x与u,y与v的关系,代入G的轨迹方程进而可得A的轨迹方程.
解答:解:(I)以BC所在的直线为X轴,BC中点为原点建立直角坐标系.
设G点坐标为(x,y),
∵重心分中线比为2:1
∴|GC|+|GB|=30×
=20,
根据椭圆的定义可知G点的轨迹是以B,C为焦点的椭圆,且除去轴上两点.
因a=10,c=8,有b=6,故其方程为
+
=1(y≠0)
(II)设A点坐标为(u,v)
则x=
,y=
,把(3u,3v)代入G的方程得
+
=1(y≠0)
故顶点A的轨迹为得
+
=1(y≠0)
设G点坐标为(x,y),
∵重心分中线比为2:1
∴|GC|+|GB|=30×
| 2 |
| 3 |
根据椭圆的定义可知G点的轨迹是以B,C为焦点的椭圆,且除去轴上两点.
因a=10,c=8,有b=6,故其方程为
| x2 |
| 100 |
| y2 |
| 36 |
(II)设A点坐标为(u,v)
则x=
| u |
| 3 |
| v |
| 3 |
| u2 |
| 900 |
| v2 |
| 324 |

故顶点A的轨迹为得
| x2 |
| 900 |
| y2 |
| 324 |
点评:本题主要考查了轨迹方程的问题.本题解题的关键是利用了椭圆的定义求得轨迹方程.考查转化思想.

练习册系列答案
相关题目
 如图,已知椭圆
如图,已知椭圆 (理科做)如右图,多面体是过正四棱柱的底面正方形ABCD的顶点A作截面AB1C1D1而截得的,且BB1=DD1,已知截面AB1C1D1与底面成30°的二面角,AB=1,则这个多面体的体积为( )
(理科做)如右图,多面体是过正四棱柱的底面正方形ABCD的顶点A作截面AB1C1D1而截得的,且BB1=DD1,已知截面AB1C1D1与底面成30°的二面角,AB=1,则这个多面体的体积为( )