题目内容
已知数集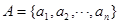 ,其中
,其中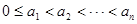 ,且
,且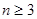 ,若对
,若对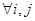 (
(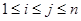 ),
),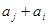 与
与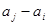 两数中至少有一个属于
两数中至少有一个属于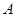 ,则称数集
,则称数集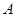 具有性质
具有性质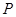 .
.
(Ⅰ)分别判断数集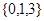 与数集
与数集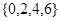 是否具有性质
是否具有性质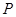 ,说明理由;
,说明理由;
(Ⅱ)已知数集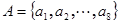 具有性质
具有性质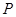 ,判断数列
,判断数列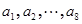 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
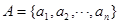 ,其中
,其中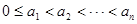 ,且
,且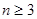 ,若对
,若对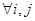 (
(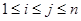 ),
),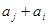 与
与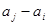 两数中至少有一个属于
两数中至少有一个属于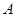 ,则称数集
,则称数集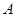 具有性质
具有性质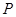 .
.(Ⅰ)分别判断数集
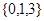 与数集
与数集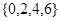 是否具有性质
是否具有性质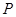 ,说明理由;
,说明理由;(Ⅱ)已知数集
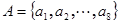 具有性质
具有性质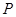 ,判断数列
,判断数列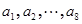 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.(Ⅰ)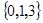 不具有性质
不具有性质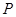 ;
;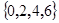 具有性质
具有性质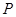 .
.
(Ⅱ)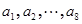 构成等差数列.
构成等差数列.
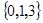 不具有性质
不具有性质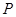 ;
;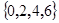 具有性质
具有性质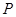 .
. (Ⅱ)
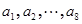 构成等差数列.
构成等差数列. 试题分析:(Ⅰ)由于
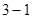 和
和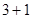 都不属于集合
都不属于集合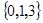 ,所以该集合不具有性质
,所以该集合不具有性质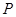 ;
;由于
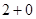 、
、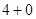 、
、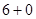 、
、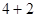 、
、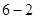 、
、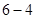 、
、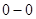 、
、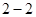 、
、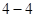 、
、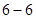 都属于集合
都属于集合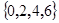 ,所以该数集具有性质
,所以该数集具有性质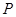 . 4分
. 4分(Ⅱ)
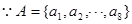 具有性质
具有性质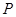 ,所以
,所以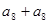 与
与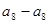 中至少有一个属于
中至少有一个属于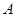 ,
,由
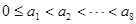 ,有
,有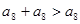 ,故
,故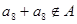 ,
,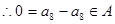 ,故
,故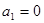 .
.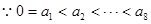 ,
,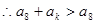 ,故
,故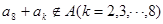 .
.由
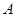 具有性质
具有性质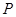 知,
知,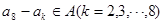 ,又
,又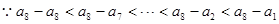 ,
,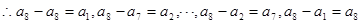 ,即
,即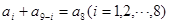 ……①
……①由
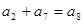 知,
知,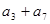 ,
,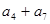 ,…,,
,…,,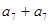 均不属于
均不属于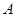 ,
,由
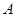 具有性质
具有性质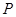 ,
,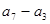 ,
,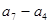 ,…,,
,…,,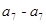 均属于
均属于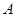 ,
,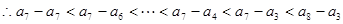 ,而
,而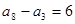 ,
,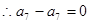 ,
,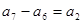 ,
,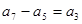 ,…,
,…,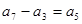 即
即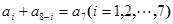 ……②
……②由①②可知
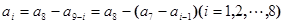 ,即
,即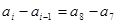 (
(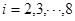 ).
).故
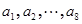 构成等差数列. 10分
构成等差数列. 10分点评:难题,本题属于新定义问题,关键是理解好给予的解题信息,并灵活地进行应用。(2)证明数列是等差数列的方法,不同于常见方法,令人难以想到。

练习册系列答案
相关题目
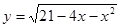 的定义域为A,函数
的定义域为A,函数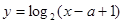 的定义域为B,(1) 若
的定义域为B,(1) 若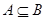 ,求实数
,求实数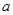 的取值范围;(2)若
的取值范围;(2)若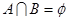 ,求实数
,求实数 ,集合
,集合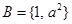 ,若
,若 ,则
,则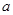 的值为 .
的值为 .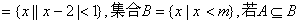 ,则m的取值范围是
,则m的取值范围是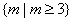
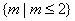
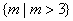
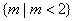
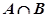 =
= 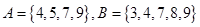 ,全集
,全集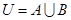 ,则集合
,则集合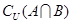 为( )
为( )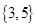
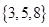
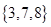
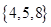
 是实数集,
是实数集, ,
, ,则
,则 .
. 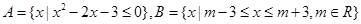
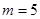 时,求
时,求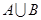 ;
;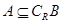 ,求
,求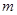 的取值范围.
的取值范围.