题目内容
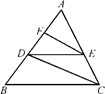
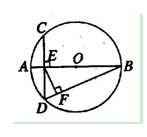
如图，圆O1与圆O2内切于点A，其半径分别为r1与r2(r1＞r2)，圆O1的弦AB交圆O2于点C(O1不在AB上)．
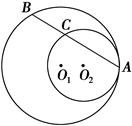
求证：AB∶AC为定值．
求证：AB∶AC为定值．
见解析
证明 如图，连接AO1并延长，分别交两圆于点E和点D.连接BD，CE.
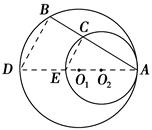
因为圆O1与圆O2内切于点A，所以点O2在AD上，故AD，AE分别为圆O1，圆O2的直径．从而∠ABD＝∠ACE＝
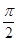.所以BD∥CE，于是
＝
＝
＝
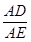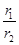.所以AB∶AC为定值．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
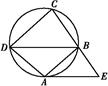
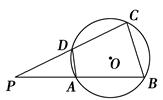
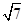的⊙O中，弦AB，CD相交于点P，PA＝PB＝2，PD＝1，则圆心O到弦CD的距离为________．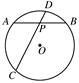
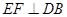，垂足为F，若
，
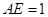，则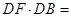
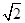，求AF的长．