题目内容
设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若对任意x∈[a，b]，
都有|f（x）-g（x）|≤1成立，则称f（x）和g（x）在[a，b]上是“紧密函数”．若
与g（x）=mx-1在[1，2]上是“紧密函数”，则m的取值范围是（ ）
A．[0，1] B．[2，3] C．[1，2] D．[1，3]
【答案】
A
【解析】因为f（x）与g（x）在[a，b]上是“紧密函数”，则|f（x）-g（x）|≤1即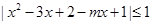
在[1，2]上成立,即|
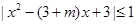在[1，2]上成立,化简得
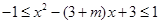在[1，2]上成立,∴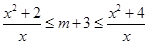
即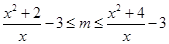
在x∈[1，2]上成立.
令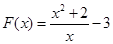
,，x∈[1，2]，则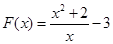在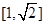
上单调递减，在
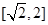上单调递增，所以F(x)的最大值为F(2)=0; 
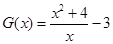在[1,2]上是减函数，所以G(x)的最小值为G(2)=1.∴0≤m≤1.
练习册系列答案
相关题目