Question

【题目】某企业招聘中，依次进行A科、B科考试，当A科合格时，才可考B科，且两科均有一次补考机会，两科都合格方通过．甲参加招聘，已知他每次考A科合格的概率均为 ，每次考B科合格的概率均为 ．假设他不放弃每次考试机会，且每次考试互不影响．
（1）求甲恰好3次考试通过的概率；
（2）记甲参加考试的次数为ξ，求ξ的分布列和期望．

Answer 1

【答案】
（1）解：设甲“第一次考A科成绩合格”为事件A1，“A科补考后成绩合格”为事件A2，

“第一次考B科成绩合格”为事件B1，“B科补考后成绩合格”为事件B2．

甲参加3次考试通过的概率为：

（2）解：由题意知，ξ可能取得的值为：2，3，4

=

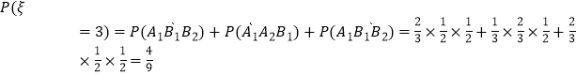
分布列（如表）

ξ	2	3	4
P

故

【解析】设甲“第一次考A科成绩合格”为事件A1 ， “A科补考后成绩合格”为事件A2 ， “第一次考B科成绩合格”为事件B1 ， “B科补考后成绩合格”为事件B2 ． （1）甲参加3次考试，是指补考一次，且合格；（2）确定ξ可能取得的值，求出相应的概率，进而可得ξ的分布列和期望．