题目内容
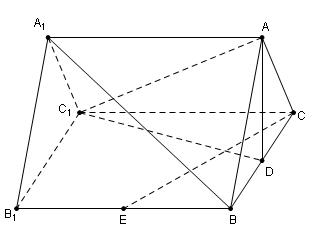
已知如图几何体,正方形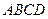 和矩形
和矩形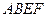 所在平面互相垂直,
所在平面互相垂直,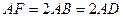 ,
, 为
为 的中点,
的中点,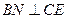 。
。
(Ⅰ)求证: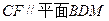 ;
;
(Ⅱ)求二面角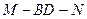 的大小
的大小
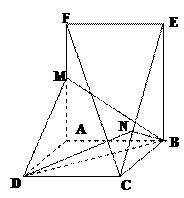
 和矩形
和矩形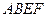 所在平面互相垂直,
所在平面互相垂直,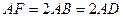 ,
, 为
为 的中点,
的中点,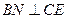 。
。(Ⅰ)求证:
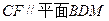 ;
; (Ⅱ)求二面角
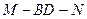 的大小
的大小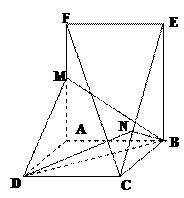
(I)证明:连结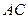 交
交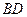 于
于 ,连结
,连结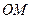
因为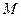 为
为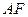 中点,
中点,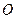 为
为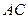 中点,
中点,
所以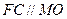 ,
,
又因为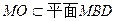 ,
,
所以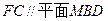 ; …………………4分
; …………………4分
(II)因为正方形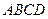 和矩形
和矩形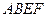 所在平面互相垂直,
所在平面互相垂直,
所以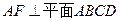
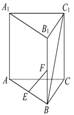
以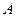 为原点,以
为原点,以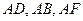 为
为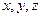 轴建立空间直角坐标系,如图取
轴建立空间直角坐标系,如图取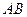 =1
=1

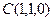 ,
,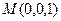 ,
,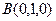 ,
,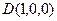 ,
,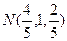
设平面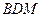 的法向量为
的法向量为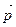 =" (x" ,y , z ),
=" (x" ,y , z ),
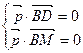
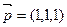 ……6分
……6分
设平面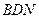 的法向量为
的法向量为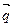 =" (x" ,y , z ),
=" (x" ,y , z ),
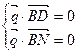
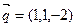
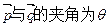 …………………8分
…………………8分
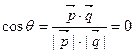
所以二面角 的大小为
的大小为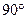 。
。
 交
交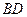 于
于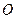 ,连结
,连结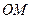
因为
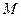 为
为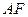 中点,
中点,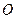 为
为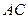 中点,
中点,所以
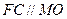 ,
,又因为
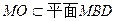 ,
,所以
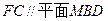 ; …………………4分
; …………………4分(II)因为正方形
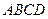 和矩形
和矩形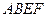 所在平面互相垂直,
所在平面互相垂直,所以
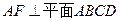
以
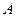 为原点,以
为原点,以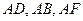 为
为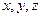 轴建立空间直角坐标系,如图取
轴建立空间直角坐标系,如图取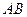 =1
=1
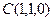 ,
,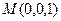 ,
,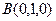 ,
,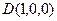 ,
,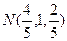
设平面
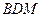 的法向量为
的法向量为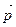 =" (x" ,y , z ),
=" (x" ,y , z ), 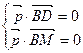
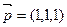 ……6分
……6分设平面
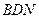 的法向量为
的法向量为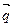 =" (x" ,y , z ),
=" (x" ,y , z ), 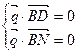
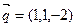
 …………………8分
…………………8分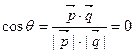
所以二面角
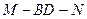 的大小为
的大小为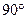 。
。略

练习册系列答案
相关题目
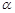 ∩平面
∩平面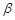 =AB,PQ⊥
=AB,PQ⊥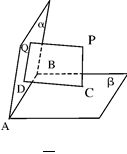
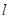 、
、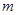 与平面
与平面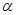 和
和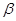 的命题中,真命题的是( )
的命题中,真命题的是( )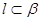 且
且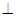
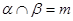 且
且

 中,底面
中,底面 是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.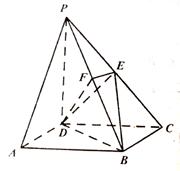
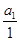 =
=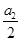 =
=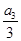 =k,则
=k,则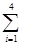 (ihi)=
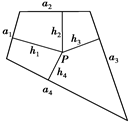
(ihi)=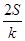 .类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若
.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若
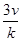
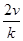
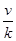
 本小题满分12分)如图,在三棱柱
本小题满分12分)如图,在三棱柱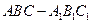 中,
中, 面
面 ,
,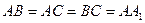 ,
,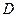 ,
,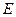 分别为
分别为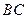 ,
,
 的中点.
的中点. ∥平面
∥平面 ; (2)求证:
; (2)求证: 平面
平面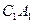 与平面
与平面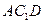 所成的角的
所成的角的 正弦值.
正弦值.