题目内容
(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
如题(19)图,在四棱锥 中,
中,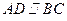 且
且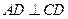 ;平面
;平面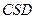
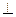 平面
平面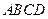 ,
,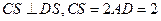 ;
;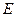 为
为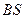 的中点,
的中点,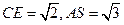 。求:
。求:
(Ⅰ)点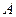 到平面
到平面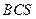 的距离;
的距离;
(Ⅱ)二面角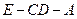 的大小。
的大小。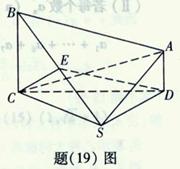
如题(19)图,在四棱锥
 中,
中,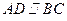 且
且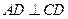 ;平面
;平面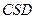
 平面
平面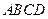 ,
,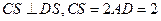 ;
;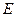 为
为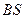 的中点,
的中点,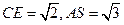 。求:
。求:(Ⅰ)点
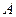 到平面
到平面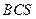 的距离;
的距离;(Ⅱ)二面角
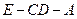 的大小。
的大小。
(Ⅰ)
(Ⅱ)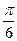

(Ⅱ)
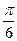
解法一:(Ⅰ)因为AD//BC,且
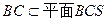 ,所以
,所以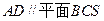 ,从而A点到平面
,从而A点到平面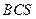 的距离等于D点到平面
的距离等于D点到平面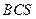 的距离。
的距离。因为平面
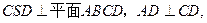 故
故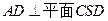 ,从而
,从而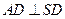 ,由AD//BC,得
,由AD//BC,得
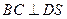 ,又由
,又由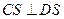 知
知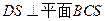 ,从而
,从而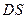 为点A到平面
为点A到平面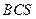 的距离,因此在
的距离,因此在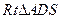 中
中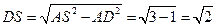 。
。(Ⅱ)如答(19)图1,过E电作
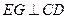 ,交
,交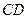 于点G,又过G点作
于点G,又过G点作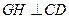 ,交AB于H,故
,交AB于H,故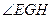 为二面角
为二面角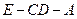 的平面角,记为
的平面角,记为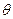 ,过E点作EF//BC,交
,过E点作EF//BC,交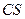 于点F,连结GF,因平面
于点F,连结GF,因平面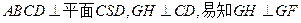 ,故
,故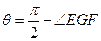 。
。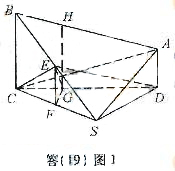
由于E为BS边中点,故
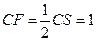 ,在
,在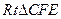 中,
中,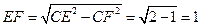 ,因
,因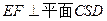 ,又
,又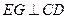 ,
,故由三垂线定理的逆定理得
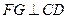 ,从而又可得
,从而又可得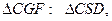
因此
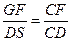 而在
而在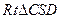 中,
中,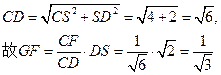
在
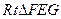 中,
中,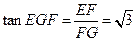 可得
可得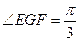 ,故所求二面角的大小为
,故所求二面角的大小为 。
。解法二:
(Ⅰ)如答(19)图2,以S(O)为坐标原点,射线OD,OC分别为x轴,y轴正向,建立空间
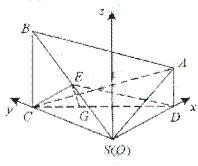
坐标系,设
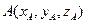 ,因平面
,因平面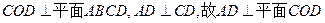
即点A在xoz平面上,因此
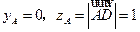 。
。又
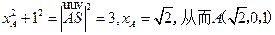 ,
,因AD//BC,故BC⊥平面CSD,即BCS与平面yOx重合,从而点A到平面BCS的距离为
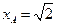 。
。(Ⅱ)易知C(0,2,0),D(,0,0)。因E为BS的中点,ΔBCS为直角三角形,
知
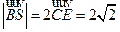 。
。设B(0,2,
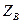 ),
),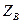 >0,则
>0,则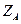 =2,故B(0,2,2),所以E(0,1,1)。
=2,故B(0,2,2),所以E(0,1,1)。在CD上取点G,设G(
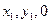 ),使GE⊥CD。
),使GE⊥CD。由
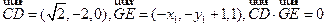 故
故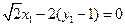 ①
① 又点G在直线CD上,即
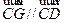 ,由
,由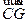 =(
=(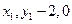 ),则有
),则有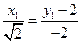 ②
②联立①、②,解得G=
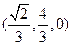 ,
,故
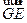 =
=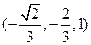 ,又由AD⊥CD,所以二面角E-CD-A的平面角为向量
,又由AD⊥CD,所以二面角E-CD-A的平面角为向量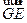 与向量
与向量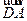 所成的角,记此角为
所成的角,记此角为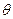 。
。因为
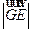 =
=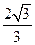 ,
,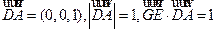 ,所以
,所以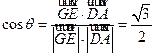 ,故所求的二面角的大小为
,故所求的二面角的大小为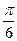 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
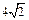 的正三角形
的正三角形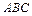 中,
中,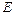 、
、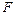 分别为
分别为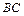 和
和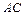 的中点,
的中点,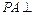 面
面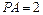 ,设平面
,设平面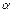 过
过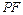 且与
且与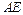 平行。 求
平行。 求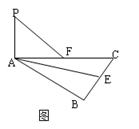
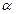 ,BC∥
,BC∥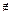
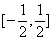
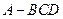 中,
中,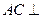 底面
底面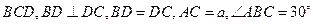 ,点
,点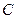 到平面
到平面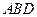 的距离是( ).
的距离是( ).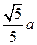

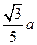
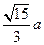

 平面
平面 ,直线
,直线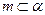 ,直线
,直线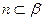 ,点
,点 ,点
,点 ,记点
,记点 之间的距离为
之间的距离为 ,点
,点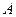 到直线
到直线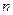 的距离为
的距离为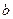 ,直线
,直线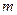 和
和 ,则( )
,则( )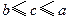

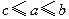

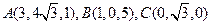 ,则AB的中点M与C的距离为_ ▲ .
,则AB的中点M与C的距离为_ ▲ .