题目内容
函数f（x）=cos（π-x）•lg|x|在区间
内的图象是
- A.
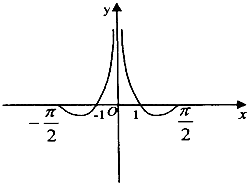
- B.
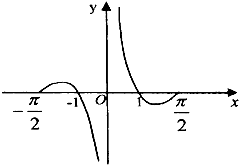
- C.
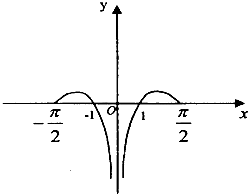
- D.
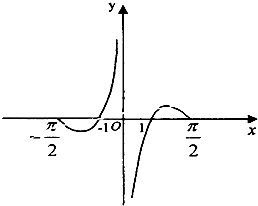
A
分析：先利用诱导公式化简函数f（x），再利用偶函数的定义，判断函数的奇偶性，排除两个选项，最后利用特殊值代入法，得正确选项
解答：∵函数f（x）=cos（π-x）•lg|x|=-cosx•lg|x|
∴f（-x）=-cos（-x）•lg|-x||=-cosx•lg|x|=f（x）
∴函数f（x）为偶函数，排除B、D
∵f（
）=-cos•lg||＞0，排除C
故选 A
点评：本题考查了函数的奇偶性定义及其图象特点，诱导公式及排除法解图象选择题
分析：先利用诱导公式化简函数f（x），再利用偶函数的定义，判断函数的奇偶性，排除两个选项，最后利用特殊值代入法，得正确选项
解答：∵函数f（x）=cos（π-x）•lg|x|=-cosx•lg|x|
∴f（-x）=-cos（-x）•lg|-x||=-cosx•lg|x|=f（x）
∴函数f（x）为偶函数，排除B、D
∵f（
）=-cos•lg||＞0，排除C故选 A
点评：本题考查了函数的奇偶性定义及其图象特点，诱导公式及排除法解图象选择题
练习册系列答案
相关题目